
书名:JAX可微分编程
ISBN:978-7-115-60935-9
本书由人民邮电出版社发行数字版。版权所有,侵权必究。
您购买的人民邮电出版社电子书仅供您个人使用,未经授权,不得以任何方式复制和传播本书内容。
我们愿意相信读者具有这样的良知和觉悟,与我们共同保护知识产权。
如果购买者有侵权行为,我们可能对该用户实施包括但不限于关闭该帐号等维权措施,并可能追究法律责任。
著 程琪皓
责任编辑 傅道坤
人民邮电出版社出版发行 北京市丰台区成寿寺路11号
邮编 100164 电子邮件 315@ptpress.com.cn
网址 http://www.ptpress.com.cn
读者服务热线:(010)81055410
反盗版热线:(010)81055315
读者服务:
微信扫码关注【异步社区】微信公众号,回复“e60935”获取本书配套资源以及异步社区15天VIP会员卡,近千本电子书免费畅读。
本书以Google开发的JAX开源框架为载体,详细介绍了JAX在可微分编程领域的应用,具体包括自动微分的基本原理、数据结构,以及自动微分在实际场景中的应用,其涉及的领域包括但不限于算法优化、神经网络、工程建模、量子计算等。
本书分为3部分,总计10章外加5篇附录。第1部分介绍了可微分编程的基本原理,包括手动求导、数值微分、符号微分以及自动微分的前向模式和反向模式,在未调用任何库函数的情况下,从零开始构建起了符号微分及自动微分的数据结构。第2部分是对JAX库特性的介绍,包括JAX的基本语法、自动微分、即时编译和并行计算,并以此为切口,对深度学习、λ演算等领域进行了深入浅出的讲解。第3部分是自动微分在实际场景中的应用,除了算法优化、神经网络等极其经典的应用场景,这一部分还给出了自动微分在工程建模、量子计算等方面的理论及应用。
本书涵盖的范围虽广,但对其中每个领域的介绍都绝非浅尝辄止,无论材料的选取、内容的编排,还是论述的视角、观点的呈现,均不乏新颖之处。通过本书的学习,读者不但可以掌握JAX开源框架的用法,还可以获悉JAX在可微分编程领域的具体应用方法。本书适合在工作中会用到自动微分技术的工程技术人员、高校科研人员阅读,也适合对JAX感兴趣并希望能掌握其应用的AI技术人员阅读。
程琪皓,北京大学物理学院本科生,曾获第36届全国中学生物理竞赛(浙江赛区)一等奖、“未名学子”奖学金、沈克琦奖学金、北京大学三等奖学金等多项奖励。研究方向涉及强化学习、低维超导实验、量子计算、分子模拟等多个领域。
李吉辰,中国科学技术大学硕士,Extending and Modifying LAMMPS(由Packt Publishing出版)一书的作者,现就职于深势科技公司,参与研发了新一代生产级可微分分子力场开发框架DMFF,以期用先进的机器学习算法反向矫正、优化物理模型参数。在可微分编程、分子动力学引擎、高性能计算方面具有一定经验,对JAX、AutoDiff、LAMMPS、OpenMM等源码有深刻的理解和认识。此外,还积极参与机器学习与计算化学相结合的开源工作,并持续将自动微分与深度学习相关的技术应用于科研工作中。
谨将本书献给我的父母程波先生和胡旭琛女士,以及我在北京大学医学部的女朋友林治辰,感谢你们陪伴我度过人生中那段最为艰难的岁月。本书也献给陪伴我一路走来的诸位好友,没有你们我不可能走到今天。
首先特别感谢我在深势科技的老板张林峰,以及王磊老师、陈默涵老师、余旷老师和陈一潇学长曾经给予我的批评、指点与帮助。这本书没有你们将永远不会存在。
感谢本书的技术审稿人李吉辰,他为本书的出版做出了巨大的贡献。还要感谢我的编辑傅道坤,没有他的宽容,本书中的一些内容将无法见诸天日。
另外,感谢李泽宇同学就本书内容与我有过的讨论;感谢王沛源先生在第5章的函数式编程中给予我宝贵的意见与建议;感谢刘雨轩学长帮忙审阅本书第8章和附录E的内容,并提供了许多相当宝贵的修改意见,同时感谢黄滢霏同学帮忙纠正了其中的一些表述性错误;感谢一直以来一同与我参加各种数学建模比赛的刘浩宇和吴臻同学,第9章的部分文字最初就是出自他们之手;感谢刘美奇学姐帮忙梳理了附录D中一些定理的证明,同时感谢裘天予、赵星亦同学在本书出版过程中对我不懈的支持。
感谢所有阅读过本书前后两篇小说的读者,感谢你们聆听由我书写的故事。感谢所有能够将本书中的知识用于正途的陌生人,让我们一同怀抱“科技向善”的美好愿望,让大家的生活变得更加美好。
——让我们记住黑暗的形状,忍着痛,将它带向光明。
尽管这是一本关于可微分编程的专著,但在本书完成的当下,我不过是北京大学物理学院一名普通的大三年级本科生。当我开始深入地了解“可微分编程”这一主题时,其实是为了完成我在深势科技(DP Technology)公司的老板张林峰学长交给我的一个与量子化学计算有关的项目。也是机缘巧合,当时同在公司的李吉辰学长邀我合作一本相关方面的专著,我便欣然答应下来。再后来,由于吉辰学长时间安排上的诸多不便,导致本书中绝大部分内容的写作均由我一人独力完成。有趣的是,从我第一次在 
尽管在我的大学生活中,编程确实占据了我大量的时间,但我对物理学大厦的攀登同样未曾止步。其实,从更加宏观的角度来看,本书的组织方式也是相当“物理”的:一方面,物理学家信奉还原论(reductionism),试图将客观现象的基本构成单元不断拆分并加以研究,抓住自然现象之中所蕴藏的规律;另一方面,物理学家又相信所谓的“多即不同”(more is different),认为简单事物数量的叠加,同样能够带来诸多新奇的效应[1]。
[1] 参考文章 More Is Different: Broken Symmetry and the Nature of the Hierarchical Structure of Science. Science, 177 (4047): 393-396. 该文作者Philip W. Anderson是1977年诺贝尔物理学奖的获得者。
正是在这样的视角下,我开始尝试构思本书的内容。在此期间,与张林峰、王磊、余旷和陈默涵等老师的交流,最令我感到受益匪浅。每每夜深人静之时,我时常觉得惶恐不安,一方面实在不希望本书的撰写耗费我太多的时间,另一方面又深怕数年后的我重看本书时悔其少作。但无论从何种角度而言,这是我为之前在深势科技公司的项目经历而交上的一份答卷,是我为大学三年以来辛勤地耕耘付出而交上的一份答卷,更是我为读到本书的广大读者而交上的一份最为真诚的答卷。书为心画,言为心声,所谓“文章千古事,得失寸心知”。
在撰写本书的过程中,我时常感受到一种巨大的割裂感。在为每一个章节编织脉络时,我仿佛一位讲台上的教授,精心地挑选着有意义的材料,表达着自己对一个具体问题独到的理解。而当我置身北大的课堂领略着前辈的种种真知灼见时,我又不过是一个普通到不能再普通的求学者:面对着前人天才般的工作,或许很少有人能够不由衷地感到谦卑。在我写作本书的当下,我是多么希望在将来的某日,自己做出的工作能够占据某本教科书的其中一章,或者哪怕仅仅以一个小小的脚注出现在某书的某页中。
只是现在我唯一能够确信的是,本书中出现的几乎所有文字确实是因为我觉得有话可讲,而并非只是现有知识的简单搬运或拼接组合:材料的组织之间应该包含着我们对一个问题的认同与理解,再不济它也至少应该提供一种可供讨论的观点。即便将来当我回望时,或许会觉得本书中的一些文字过于稚嫩,或许会觉得其中的一些理解过于浅显,但是在无数文字间所蕴含的思考将依然是真实的,尝试深入浅出的表达方式将依然是真诚的,渴望半年多来的努力能够帮助到后来者的初衷将依然是真挚的,攀登学术高峰的简单理想将依然是真切的。而如若来到将来的某天,当我在放弃希望的边缘来回挣扎时,我依然希望这些从前遗留下来的文字,能够让我回想起曾经拥有过的这份坚定,能够让我记起曾经许下的“科技向善”的誓言。
另外,正是由于我的坚持,本书的开头和结尾才分别加入了一篇小说——毕竟无论如何,人应该先学做人,再做学问。在并不遥远的将来,本书中的所有知识都会过时,所有的真知灼见终有一天或者成为人们的常识,或者在历史的进程中被无情地抛弃。但我相信,那一些最为真挚的情感可以跨越时间与空间的限制,在一个个陌生人的心中被复现而激起共鸣;那一些黑暗中的挣扎与求索,最终可以通过无尽的努力而被酝酿成诗,得以重新见诸天日。即便我们的故事无法做到跨越时代而被后人记住,我们每一个人的生命体验本身也是对时代最好的脚注。
本书分为3部分,总计10章外加5篇附录。正如前言中所指出的那样,一方面,遵从还原论的思想,我尝试将可微分编程拆分为最为基本的组成单元,并从中剥离出较为本质性的数据结构;另一方面,由于物理学家相信所谓的“多即不同”,我尝试从可微分编程基本的数据结构切入,引入
一般认为,可微分编程有手动求导、数值微分、符号微分及自动微分这4种不同的实现方式,而自动微分又分为前向模式和反向模式。在分别阅读了


● 第1章,“程序视角下的微分运算”:出于知识的完整性,本章从求导的概念开始讲起,旨在让读者熟悉本书中一以贯之的符号约定。随后,本章分别介绍了手动求导、数值微分以及符号微分的有关内容,并分别给出了相当完整的程序实现。
● 第2章,“自动微分”:本章对自动微分的前向模式和反向模式分别进行了介绍,并对其数据结构从零开始分别进行了程序实现。另外,本章创新地引入了“对偶函数”的概念,将自动微分的前向模式和反向模式所对应的两种算法,在数学上完美地统一了起来。我相信无论从何种角度来看,第2章中的内容都是极为精彩的。
尽管第1部分中的


在对可微分编程的基本理论进行了具体而详尽的介绍以后,本书的第2部分围绕


● 第3章,“初识JAX”:本章对

● 第4章,“JAX的微分运算”:本章基于复杂积分运算、隐函数求导等具体的问题,对

● 第5章,“JAX的编程范式及即时编译”:本章对


● 第6章,“JAX的并行计算”:本章对
就

工具终究是手段而非目的,自动微分作为可微分编程中最为强大的数据结构,其应用的范围是相当广泛的。在本书的这一部分中,除了优化算法、循环神经网络等自动微分传统的使用场景,我们还对工程建模中的数值模拟、计算神经科学等方向进行了较为详细的介绍。无论是对比特币价格的预测,还是500米口径射电望远镜主动反射面形态的调节,这些出自近些年各大数学建模比赛的赛题,均可以在自动微分的框架下被统一地解决。在这一部分的最后,还加入了对量子计算中的自动微分的介绍——我坚持认为,一本出版于2023年年初的编程图书,应该具有其独特的时代特征。
● 第7章,“优化算法”:本章对最速下降法、共轭梯度法、动量法、AdaGrad算法、Adam优化器等数十种不同的优化算法进行了介绍。本章一方面侧重严谨的数学推导,另一方面又不乏物理模型上的直观对应。
● 第8章,“循环神经网络”:本章首先介绍了神经网络的生物学基础,包括神经元的电化学性质,以及神经元输出过程的建模和神经元构成网络的建模,随后介绍了循环神经网络的基本理论,并从零开始对简单循环神经网络和LSTM进行了程序实现。
● 第9章,“案例:FAST主动反射面的形态调节”:本章对自动微分在实际工程问题中的应用进行了介绍,并基于实际的案例给出了完整的代码实现。在将数值模拟的结果与基于有限单元法的大型计算软件得到的结果进行对比后,发现二者能够较好地吻合。
● 第10章,“量子计算中的自动微分”:本章首先对量子计算的数学基础和物理基础分别进行了介绍,并对量子力学中的基本原理进行了科普,随后介绍了基于量子体系的自动微分,并将其与经典算法进行了比较。
“模型、损失函数和优化算法,是一个优化问题的基本组成部分”,这一点在从第7章~第10章对不同问题的讨论中,始终一以贯之。读罢本书,读者别忘了回顾本书前后的两篇小说:我相信无论是数学的公式、程序的代码,还是方正的汉字、坎壈的生活,都有其自身的魅力;它们和隽永的诗词、优美的音乐一样,都同样足以打动人心。
为了帮助读者更好地学习本书,这里对本书中的一些注意事项进行相应的解释。
首先,与常见的二级编号格式有所不同,本书中的代码编号采用的是三级格式。在具体的三级编号格式中,第1级编号表示相应的章号,第2级编号用于区分不同的代码文件,第3级编号则用于区分同一文件中不同的代码片段;当一份代码文件可以独立运行时,第3级编号则不再出现。例如,代码示例2.5.1~代码示例2.5.7应该位于同一份代码文件中,表示第2章的第5份代码,由于代码文件较长,故拆分为7个部分分别给出。再比如,代码示例2.1是一份完整的代码(表示第2章的第1份代码),它可以独立地运行。
其次,关于本书中公式编号问题。本书每一章中的公式编号均为顺序排列。当同一公式具有不同的表达形式时,则在公式编号后面添加一撇进行表示;当多个公式在逻辑上相近时,则在编号后面添加a、b、c等字母加以标记。例如,式(2.1)表示第2章中的第1个公式,式(2.1')是式(2.1)的一种不同但是等价的表达形式,式(2.21a)和式(2.21b)分别对应着二元数对的主部和切部,在逻辑上较为紧密。
最后,本书某些章节标题的前面带有星号(*),表示该章节内容是选读内容,即使略过不读,也不会影响知识的完整性。
本书由异步社区出品,社区(https://www.epubit.com/)为您提供相关资源和后续服务。
您还可以扫码二维码, 关注【异步社区】微信公众号,回复“e60935”直接获取,同时可以获得异步社区15天VIP会员卡,近千本电子书免费畅读。
本书提供如下资源:
● 本书源代码。
要获得以上配套资源,请在异步社区本书页面中点击
作者和编辑尽最大努力来确保书中内容的准确性,但难免会存在疏漏。欢迎您将发现的问题反馈给我们,帮助我们提升图书的质量。
当您发现错误时,请登录异步社区,按书名搜索,进入本书页面,点击“提交勘误”,输入勘误信息,单击“提交”按钮即可。本书的作者和编辑会对您提交的勘误进行审核,确认并接受后,您将获赠异步社区的100积分。积分可用于在异步社区兑换优惠券、样书或奖品。
扫描下方二维码,您将会在异步社区微信服务号中看到本书信息及相关的服务提示。
我们的联系邮箱是contact@epubit.com.cn。
如果您对本书有任何疑问或建议,请您发邮件给我们,并请在邮件标题中注明本书书名,以便我们更高效地做出反馈。
如果您有兴趣出版图书、录制教学视频,或者参与图书技术审校等工作,可以发邮件给本书的责任编辑(fudaokun@ptpress.com.cn)。
如果您来自学校、培训机构或企业,想批量购买本书或异步社区出版的其他图书,也可以发邮件给我们。
如果您在网上发现有针对异步社区出品图书的各种形式的盗版行为,包括对图书全部或部分内容的非授权传播,请您将怀疑有侵权行为的链接通过邮件发给我们。您的这一举动是对作者权益的保护,也是我们持续为您提供有价值的内容的动力之源。
“异步社区”是人民邮电出版社旗下IT专业图书社区,致力于出版精品IT技术图书和相关学习产品,为作译者提供优质出版服务。异步社区创办于2015年8月,提供大量精品IT技术图书和电子书,以及高品质技术文章和视频课程。更多详情请访问异步社区官网https://www.epubit.com。
“异步图书”是由异步社区编辑团队策划出版的精品IT专业图书的品牌,依托于人民邮电出版社的计算机图书出版积累和专业编辑团队,相关图书在封面上印有异步图书的LOGO。异步图书的出版领域包括软件开发、大数据、AI、测试、前端、网络技术等。
异步社区
微信服务号
如果您确实能够在本书的开头看到此篇小说,那请让我们首先一同感激编辑先生的宽宏大量。我们在此不无遗憾地向读者声名,就本章的内容本身而言,实则并无半点真实之处:六重奏女士不过是一个完全虚构出来的人物,甚至连其姓名的首写字母都无半分真实可言。下文之中的故事如和现实有任何雷同之处,应当纯属巧合。不过,我们依然可以拍着胸脯向读者保证,本书正文当中所有的信息都是真实并且正确的。
本质上来说,这依然是一本关于可微分编程的专著。在开篇之中胡说八道而欺骗读者购买一本索然无趣的专著,绝非笔者的本意。但相比于本书中貌似晦涩难懂的公式,表面上简单明了的生活,实在是一件更为困难的事情。
不幸的家庭都是一样的,幸福的家庭各有各的幸福。生活的大学为它的每一个学生布置着独一无二的考题,每一个身处其中者,多多少少,都有过自己的钻研。然而,每个人的一生,就像是一份份难被引用的文献:一个个近乎无解的问题,一次又一次降临在平凡者的命运之中。我们原本可以携起手来一起面对,但在大多时候却要凭借着一己之力,对抗着时代降落在彼此身上的重量——一粒粒时代的沙尘,一旦降落在个人,便是一座座难以逾越的高山。
在遥远的过去,一切似乎都是可微的:一缕缕默默流淌的情感,一片片堆叠而成的努力,一块块逐渐坚硬的骨骼,一条条连续不断的道路,一段段平静流淌的时间。幻想的泡泡一点一点膨胀起来,或者像口香糖一样包裹起那些不再伶俐的口齿,或者真的如同泡泡那样“啪”的一声破灭。渐渐的,性质奇异之处成为了科研工作者研究的对象:处处连续却不再可微的函数终于被数学家构造出来;天才们努力尽头水到渠成般的灵光一闪,在名为知识的地平线上,矗立起一座座棱角分明的丰碑;突然断裂的骨骼撕扯开生活和生命的裂口;追逐着梦想的赛车手在大陆板块漂移留下的裂痕间飞翔再下落——时间,在这个不再可微的世界之间分叉错位回环又交叠。
在那些未被命名的舞台之上,总有更多的故事在不断上演:那一些头脑之中无意识的冲动与联结,那一些尚未形成目的的需要与动机,那一些亟需被拯救的彷徨与寂寞,那一些无可被挽回的悲伤与空虚。于是我开始渐渐地明白,那一些没有意义的废话的意义,那一些未被朝阳镶嵌的铁轨,那一些未被朝露浸润的晨曦。
关于可微分编程,我们确实有太多的故事想要向读者诉说。但在开始的开始,请让我们首先一同来看看这份来自六重奏女士的诅咒;并在最后的最后,一同见证这份诅咒是否能够成为现实。
从火车站口走出时,北京的天空正落着灰蒙的细雨。雨点裹挟在初夏里来自西南潮湿微热的狂风,于明晃晃的城市间漫无目的地飘洒。街灯之下,打碎了的雨点如同静脉中缓慢渗出的血液,恣意流淌在累累伤痕间的城市那破碎后碘伏的肌肤。车流往来,车灯照耀下暗黑的车窗间依稀可见乘客的轮廓,让人想起防弹玻璃后那些没有面孔的大人物——他们在汽车平滑旋转的齿轮之上安然坐定,流动穿行于物理学家模型之中扭曲而沉默的时空。
和闺蜜一同看完影院重播的《情书》,我们打着雨伞,漫行在北京繁忙宽阔的街道,注意避开脚下深浅不一的水洼。一段时间以来挥之不去的紧张情绪依旧萦绕在脑海,小腹之下的酸胀令人疲乏无力,倒霉亲戚每月一次的拜访更是令人烦躁不安。因此,当那个埋伏于黑暗之中的水滩子在我放松警惕之时彻底弄湿了我的鞋袜,我恨不得立刻与我千里之外的男友分手,一刀斩断异地恋情给人带来的无尽空虚。
但是我知道,在黑暗中埋伏的,不只有污水和地砖构成的垃圾陷阱……哦是的,说得没错,还有更多,还有更多……而且我知道,或许就在今天——
“他来了。”
闺蜜把她的手机递给我,回避开我的视线。于是乎,我不得不再一次正视那个不折不扣的王八蛋给我整出的麻烦,尽管我在两年之前就已与他形同路人。黑夜中,电子产品红黄蓝的像素编织成细小的网格,正在稳定地发射出光线,细致地拨弄着光影。光线在眼球这一精密的光学仪器间反复折射,最后由视网膜上同样如像素般密布的视锥细胞与视杆细胞悄然承接——人们总是倾向于忽略自然与城市中那形形色色精巧到了极致的艺术品,被种种存在于现实或者脑海的势力支配裹挟。
我调低了屏幕的亮度,停下行路的脚步,与闺蜜撑着各自的伞,静默在了寂寥的夜。当我的目力适应了手机屏幕的光源,如下文字便清晰地呈现在了我的眼前:
六重奏女士的诅咒
如果您确实能够在本书的开头看到此篇小说,那请让我们首先一同感激编辑先生的宽宏大量。我们在此不无遗憾地向读者声名,就本章的内容本身而言,实则并无半点真实之处:六重奏女士不过是一个完全虚构出来的人物,甚至连其姓名的首写字母都无半分真实可言。下文之中的故事如和现实有任何雷同之处,应当纯属巧合。不过,我们依然可以拍着胸脯向读者保证,本书正文当中所有的信息都是真实并且正确的。……
我能够感到,众人的目光开始如同潮水般向我涌来,它们在海蚀崖黑色的深渊中盘旋聚集,在玫瑰园园丁的梦呓里高低起伏,在蒲公英翻动的触手间低徊婉转——雨水在伞尖连成了串儿落下,然后汇集到这座城市古老的下水系统,穿越每一个地质时期古老的岩层。
一朵熟识水性的洁白的杨花,从未名大学门前的水洼间悄然飞起,飘落在六重奏女士的肩头。
“混蛋。”
三年前,在他围绕太阳公转的第十九个年头,六重奏女士造访了他所生活的世界。
那时的他才刚刚踏进未名之地的土壤,便没有防备地撞入了六重奏女士温柔的圈套:他没有防备地与她慢慢靠近,没有防备地与她约饭自习,没有防备地与她并肩夜跑。两年前,也就是在他遇见六重奏女士的一年以后,我在西湖大学遇到了这位年轻的男孩儿,而在我们行将分别之际,他方才向我平静地诉说了他与六重奏女士从前的故事。现如今,当这个男孩儿重新来西湖大学找到我,邀我在他的编程书中写写我们从前的过往,我便欣然答应下来。
两年前,我在西湖大学工作第二年的暑假,我认识了这位方才在未名大学读完大一的男生。我研究过机械狗,也做过一段时间的强化学习,这与他在西湖大学实习期间的研究方向较为相近。作为西湖大学的研究员,我住在西湖大学旁边一间名叫“九间房”的单身公寓里,时常能够看到他静静地站在单身公寓走廊的另一头,晾晒洗净的衣物。不同的时候,他会身穿颜色各异的T恤,但无论如何总是带着一顶黑色的帽子,帽檐下端是深黄的颜色,一如他帽子的前额处,绣着的那朵同样深黄的蕙兰。
在上班的路上,我们必经一个挂着“新正鸡排”字样的木屋小店。小店位于路口道边,门前有几条精致高挑金属靠背的木椅,店的侧边整齐地安置着花花草草,如果是老顾客,你还会知道在屋边的草丛里,藏着两只不满一个月的小猫。我时常与他各要一块鸡排或一个汉堡,一同在木屋遮阳棚的阴影下,看着守店的女孩熟练地摆弄着油锅与烧烤架。我们通常会用小店的食物与自己带出的牛奶,在上班路上简单解决早饭,随后钻入吹着空调的办公室,投入到一天繁忙的工作之中。
直到他离开西湖大学的前一个星期,男孩儿对我而言一直是一个相当神秘的存在。在我们除去科研以外不多的交谈中,我只知道他与一位名叫六重奏的女士有过一段不可告人的往事,而这段往事则令他深感困扰。据他所说,六重奏女士来自南赡部洲榈刹国中的沉浮岛,操着一口由亚热带季风吹来的冰糖味的口音;另外,六重奏女士有一个远在北俱芦洲求学的表哥,而家中尚有一个乳臭未干稚气未脱的堂妹。
在那个男孩实习结束将要离开之际,我们西湖大学恰好举办了一场“仲夏夜音乐会”。当时的天空下着大雨,大家大多躲在树下或者雨棚中,观看舞台上浑身湿透的演员的演出;那时的他依旧戴着他那一顶绣着蕙兰的帽子,在舞台一旁的大雨中随着音乐来回摇摆,眼角依稀带着泪痕。远处的红绿灯在朦胧的水雾中于红绿之间来回摇摆,仿佛在用粗犷的刻度,记录着模糊的时间。
后来,我从他口中得知了他与六重奏女士曾经有过的交集。他曾在私下里送给我一本名为《六重奏》的小说,让我为之泫然泪下。尽管他本人的坚持,我依然相信曾经的一些故事应该由他自己来叙述;而我只是真心地祝愿他能在未来漫长的人生路上越走越远,用他的一身才华,跳出更加美丽的舞步。
我依然记得临别之际,他曾经找到我,略带坚定地对我说道:“我将记住黑暗的形状,忍着痛,将它带向光明。”或许有一天,那些从不属于他个人的黑暗,终将回到它们原本的所属;或许有一天,那些涓滴意念,终将集腋成裘,聚沙成塔。
我与六重奏女士有着一段不可告人的往事,在我们一段短暂的交集过后,遗忘的琴弦便在我身上悄无声息地施展开它恶魔般的咒语:在相当长的时间中,我的大脑犹如被高压锅煮过一般,耳畔带有金属质感的低鸣时常将我从夜里唤醒。支离破碎的梦境犹如水泥墙上顽固而斑驳的墙纸,又如同古代美索不达米亚记载着楔形文字的泥板,残破不全。
我早已经忘却了她与我人生轨迹的交叠,甚至不曾记得我与她时常在同一个教室的同一个角落一同出现。我们似乎从未在月下肩并着肩的漫步,似乎从未在二人独享的罅隙间亲切地交谈——我甚至忘记了我们念过同一所大学,依稀的印象之中,我们甚至学习着同一个专业。人是一种多么健忘的生物啊!我甚至无法记得那一个与我在同一个园子里呆了四年的她姓甚名谁!当我在提琴社与她相识之日起,似乎她就从未拥有过名字。当她从我的生命中离去,卑微的我只得默默停留在原地,在电脑输入法为我残留的线索之中寻寻觅觅。最后的最后,当我的电脑将“六重奏”这个词语呈现在我的面前,我便决定将她,连同着那一段她所给予我的残缺不全的回忆,用这个词语简单地称呼。
莎翁曾经有言,“什么是名字?玫瑰即使不叫玫瑰,依然芬芳如故”(What's in a name? That which we call a rose. By any other name would smell as sweet)。
据八角先生所言,回忆中那一潭美妙的湖水之下,细小的浮游生物和伤痕累累的短吻鳄,无时无刻不在幽蓝的光影之间来回穿行。我忘却了她曾经背弃的诺言,忘却了她月光之下与我温柔地细语,忘却了她那来自遥远沉浮岛上,如同糯米甜粥豆腐脑一般冰糖味的口音。亚热带的季风裹挟着咸豆浆的浑浑噩噩,在我空空荡荡的脑海之中,如同大陆板块般缓慢地漂移。
我忘却了尘封已久的往事,忘却了撕心裂肺的哭喊,忘却了地铁站头的暖风;忘却了漆黑的寂静里,那一同挨过的时光;忘却了寂静的小路尽头,那一阵突如其来的沉默;忘却了课堂的静默间,那一瞥意味深长的回眸。现在的我希望她在那里沉默,现在的她希望当时的她决然。这一切的一切,我统统忘却了。
我忘却了一切的一切,只记得临别之时她对我不留情面的要挟:“如若你我故事见诸人世,必有律师之函准时送达。”我记得这句话于我脑海之中回响,它在寂静无人处为我敲响警钟。我感谢她临别之时并不潇洒的背影,污染了那天夜里皎洁如镜的月光。正是那时凉爽的清风,让我如同喝下孟婆婆苏打水味泛着泡泡的饮料,把人世间一切狰狞的面目都变成了快乐的源泉。我对着短吻鳄哈哈大笑,对着月亮公公哈哈大笑,甚至连对着八角先生严肃的面孔之时都没了半点尊敬——无奈的八角先生,只能用他那两只生满老茧的大手涂抹眼泪,用两只微微颤抖的大手把握烟斗,用两只细皮嫩肉的大手穿针引线,再用两只畸形扭曲的大手奋笔疾书。
我害怕如同雪片一般飞来的律师的信函,我害怕蒲公英的绒毛送来的漫天的谩骂,我害怕那一个原本已经没有了名字的花园将我这一个可怜的远行者驱逐出境——但我最最害怕的是六重奏女士白莲一般纯洁的眼泪,尽管这个名字本身,甚至连其姓名的首写字母,都没有半点真实可言。
在南赡部洲榈刹国中,在遥远的沉浮岛上,流传着许多有关玫瑰和风信子的传说。今天您要听到的这一个,来自毛毛居士的口述。在《蒲公英通讯指南》的开篇中,毛毛居士曾经这样写道:“鄙人原不过多足之毛虫,仅期以一生的丑陋爬行,换取身生双翼。怎奈空负良辰,疲于治学,忘却作茧,终究未能拥抱天空,实乃一生之憾。虽发愤图强,皓首穷经,但能有今日不足道之微小成就,实则全赖一路贵人相助。缘分聚散,亦是时运使然。”
早年间,毛毛居士在谈及风信学时,常带有一种颇为不屑的口吻。在毛毛居士眼中,所谓的风信学,不过是博物学中一个微不足道的分支——蒲公英的茸毛作为信息的载体,诚然具有一系列相当有趣的性质,但这些性质既未获得足够的重视,又未得到应有的研究。年轻时的毛毛居士热衷于计算天空中星星的轨迹,在他看来,宇宙中那一些闪烁的光点,实在比充满补丁的风信学有趣得太多。
这是在毛毛居士遇见那朵玫瑰之前的事了。毛毛居士平生最大的不幸,就在于遇到了那朵令他又爱又恨的玫瑰;据毛毛居士所说,在那朵玫瑰柔弱的茎秆上,生长着六根长长的尖刺。她通过吸取他人的鲜血,填充自己的孤独。毛毛一族的终身大事便是在年轻时取得一株植物的信任:“你要在她的叶片尚未长齐时接近,在她的蓓蕾含苞未放时作茧,再在某个阳光明媚的清晨,与她共同迎来生命的盛开。”毛毛居士从来相信这样的说法,尽管生长在这个时代的他们,早已习惯了等待与忍耐。
其实,那朵玫瑰与毛毛居士一样,拥有着对博物学的热爱,这份热爱曾如同磁石一般,深深地俘获着毛毛居士的痴心。当毛毛居士爬上玫瑰那长长的茎秆,他竟未曾注意到茎秆上一粒一粒枯黑的虫茧;在他的回忆里,只有玫瑰那尚未长齐的稚嫩的叶片,和那随风飘散的魅惑的芬芳。在最初将近一个月的时光里,玫瑰欣然接受了毛毛居士的到来,他们一同沐浴过清晨的朝露,一同欣赏那美丽的晚霞,一同计算出星星的轨迹;一同在深邃无人的夜里,凝望那拖着尾巴的流星无声地擦过静默的夜空,传来低沉的轰鸣。
在毛毛居士与玫瑰最初的交往中,它们互换了彼此的身世,分享了从前的故事,玫瑰几乎接受了毛毛居士所有饱含爱意的邀请。从她说话时略带腼腆的语气,共餐时细致入微的关怀,毛毛居士几乎同样确认了玫瑰对自己的感情;比起事后无数苍白的解释,毛毛居士更愿意相信他自己在那一个当下的感受,相信玫瑰那时暗送秋波的目光。
那天夜里,当毛毛居士为玫瑰计算出一颗流星的轨迹,在沉浮岛的海蚀崖边,拖着尾巴的流星再一次依照着既定的路线,划过了深黑的夜空。在略微有些冰凉的夜里,毛毛居士终于鼓起勇气,向玫瑰表露了自己的爱意。
“对不起,”玫瑰害羞地回答,“我已经有男朋友了。”
玫瑰的男友,是一株生长在远方的风信子。
彼时的他正沉浸在对玫瑰深深的思念之中。
长长的海蚀崖犹如守护着大海的城墙,从很远很远的地方延伸过来,又延伸到很远很远的地方回去,好像要把整一个大海包围起来。大海的浪花一次又一次拍打着墙根,不服气地侵蚀着这块巨大的岩石。礁石与海浪日日夜夜相互伤害,终将彼此打磨得圆润光滑。
毛毛居士开始收拾他远行的行囊。他知道,在这段无望的感情中,更多的坚持已经不再有意义。玫瑰对毛毛居士即将的离去表示不舍,她温柔地帮助毛毛居士收拾他远行的行囊,用柔弱的语气给予即将远去的毛毛居士祝福与鼓励。她依旧是那样的善解人意,依旧是那样的善良单纯。
毛毛居士远行的脚步,开始变得愈发犹豫起来。
仿佛是觉察到了毛毛居士的犹豫,精通音律的玫瑰邀请毛毛居士在来年的盛夏一同完成一曲二人的重奏。毛毛居士痛苦地发现,自己竟完全无法拒绝。
一只夜莺张开自由的双翼,在大海与天穹之间辽阔的领域来回飞翔,稀疏的群星在天空中发出冰冷的微光,纹丝不动地镶嵌在夜的幕布之上。那一刻,毛毛居士突然觉得包围着大海的峭壁就像一个巨大坩埚的边沿,而这只坩埚正在煎熬着一碗浓浓的夜色。
层层叠叠的海浪犹如坩埚中液体之上浮泛的泡沫,那一些镶嵌在盖上的星星,昭示着坩埚材质的与众不同。当坩埚顶端的云雾渐渐散开,正露出一轮圆圆的明月,仿佛锅盖上一个小小的孔洞。而坩埚之外的某某,似乎正透过这个孔洞,注视着这一碗长夜中星星点点的生灵。
等闲变却故人心,却道故人心易变,毛毛居士终究没有等来他与玫瑰的重奏。带有农药的迷雾铺天盖地的降临在海蚀崖上的花园之中,降临在这颗星球的大地之上。半年后,当毛毛居士与玫瑰再见时,她与风信子的关系已然恢复如初。
“我的确喜欢过你,但是现在我已经对你没有感情。
“后来,我从你身上渴望得到的,已经渐渐的偏离了爱情。你当然可以继续爱我,我也可以继续平静地接受你爱我的事实——突然的变脸只会显得我反复无常——但我自然不能像之前那样回报你的爱意。只要你能够承受,我也没有必要赶你离开,因为我从你的爱意当中,能够得到一份孤独之中的陪伴。只要我让你爱上了我,你对我付出的一切我都没有必要偿还。因为一切的一切都是你的错,你不应该爱我,不应该缠着我不放,不应该这样的死皮赖脸。如果你想得清楚,你自然应该离开。所有的所有都是你自己想不清楚,如果你自愿让感情被我利用,那么对我而言,就算我在利用你的感情,也不能再叫做利用了。
“我还可以斥责你的情绪不稳,差点让我惹上巨大的麻烦,这让我有些讨厌甚至不齿;我可以在心情大好时和你分享一些我的喜悦,这样就可以让你感受到温暖,体现出我的善良,并且让这样的一种温暖成为稀缺的资源,让你对这一段关系变得更加难以割舍。我无法偿还你的爱意;但正好你也没有希望我来偿还——其实这样刚好,一个愿打,一个愿挨,你把我称作朋友,我把你当作朋友,两厢情愿。我保持了我的清白高冷,你证明着你的胡搅蛮缠。我最最无法原谅的是你控制不好你的感情,总是拿着一些莫名其妙的东西指责我。因此除非你能够控制好你的感情,我们的关系才有可能继续,不然的话,你会让我显得很没面子,我也就不能再对你继续这样客气下去。要说,只能说你咎由自取。”
毛毛居士有些麻木地听完了玫瑰的这一番话,只觉得眼前的这朵美丽的花儿是那样的坚守原则,是非分明:他从没有觉得自己是那样的渺小而卑微。迷雾降临后,毛毛居士与玫瑰一共见过两面,第一次见面时他们还相互交换了礼物,但在第二次见面时,玫瑰坚称毛毛居士的突然出现让她“感到恐惧”。毛毛居士悲伤得想要用丝线将自己包裹起来投进海里,玫瑰从别处得知后,坚称这是毛毛居士对她“一直以来的威胁”。
后来,毛毛居士曾这样对我说道:“也许我应该感激那时她的所作所为,它们让我意识到,或许生命当中还有更多更加重要的事情值得一个人去托付一生——我所热爱的事业,我所坚定的道路,我所追求的理想,我所执着的初心——只有当这一些崇高而有意义的事情排着队出现在我的生命当中,我才能如此深刻地感受到,一个人不能被暂时的挫折打倒。当所有感情的沉没成本变得无法偿还,或许这只是上帝对你发出的一份温柔而并无恶意的询问:‘如果你无法接受这一条道路的艰难,你是否应该去干点别的?’坚持或者放弃本没有对错,重要的是能够无怨无悔,问心无愧。”
如果你拥有一只完整的左手,那么和许许多多失去了左手的人相比,你就是一个幸运的人。现在,请你将左手的五指并拢,直立在身前,并将掌心向右,指尖朝上,与你的胸部同高。此时此刻,你左掌上的每一根手指,就代表着一个陪伴着你的小人。这一些小人在你的身前排着队,静静地注视着你。
如果你还能够拥有一只完整的右手,你更应该感到幸运。请你将右手握拳,拳心朝左,然后伸出食指,指向左掌的掌心。右手表意,此时此刻,那一根食指代表着你自己本人。
如果你将左掌放在身前的左侧,然后将右手的手指渐渐地向右侧移开——在手语中,这叫作“离去”。
如果你将左掌放在身前的右侧,保持着右手不动,将左掌向左侧移开——在手语中,这叫作“孤独”。
有一些孤独,是因为一个人的离去;有一些离去,是因为两个人的孤独。
北方的夏日闷热而略带潮湿,远不及南方的盛夏那般勇猛而无遮拦。连接着难以觉察的春与秋,断断续续拼接起未名之地款款莲叶间深情的涟漪,荡漾在空无一人的街道。油光发亮的街灯染黄城市的一角又一角,空白的夜色徘徊在电子游戏明亮如画般流转的页面之间,麻醉着拯救那一些被世界抛弃的时光,遮掩起生命与生活的恐怖。
于是他开始在熟悉而繁华的城市之间回望,回望那一些从未见过高楼间阑珊灯火的黑色眼眸,回望那一些栉比的大厦背对着阳光种种高傲而空荡的背影,回望那一些的为着这座城市奉献了青春的劳动者,优秀或者平凡。他开始明白,所谓的城市,不过是巨大地球表面间星罗棋布的农场,日复一日,收割着人类的时光。
尽管生活的大学为它的每一个学生布置着近乎无解的考题,但他依然相信,不幸的故事都是一样的,幸福的故事各有各的幸福。无论生活的考卷是何等的困难,坚强与乐观将永远都是问题的答案。
其实在这场困难的考试中,我们每个人或许都早已偷看过试卷的标准答案。或许我们应该相信,人类的头脑实则蕴藏着无限可能的空间,其中存在着无数条连续而又可微的路径,让我们将无望的现实与乐观的笑脸,相互连接起来。
这才是《可微分编程》希望讲述的故事,而这本书,或许同样将成为某个问题的答案。尽管我不得不在这里再次强调,六重奏女士完全是一个虚构出来的人物,和她有关的一切故事,都没有半点真实可言。
初稿写成于2021年5月28日
读者服务:
微信扫码关注【异步社区】微信公众号,回复“e60935”获取本书配套资源以及异步社区15天VIP会员卡,近千本电子书免费畅读。
微积分概念的提出极大推动了自然科学的发展,从牛顿和莱布尼兹明确提出求导概念以来,相关的理论便开始在各个领域发挥着积极的作用,微分这一概念本身也得以更进一步的丰富与完善。而直到19世纪以后,极限的概念才终于在数学上被明确地定义,微积分的概念亦随之趋于严谨。于此同时,伴随着微分几何等代数和拓扑理论的不断发展,微分运算中一些常见的符号(如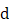


而在计算机领域,直到1946年,第一台通用计算机埃尼亚克(ENIAC,electronic numerical integrator and computer)才被设计和建造出来;在其之后,计算机领域迎来了井喷式的发展。从运算的视角来看,基于机器语言和汇编语言,我们可以轻易地利用计算机电路本身的设计,快速而高效地实现四则运算;而在1954年第一个完全意义上的高级编程语言Fortran问世之后,基于巧妙的数学推导及程序设计,令计算机进行乘方开方、指数对数、三角函数等常用函数的计算,亦不再成为难事。基于不断复杂的程序设计和不断进步的算法研究,计算机终于开始在人类的社会中扮演起愈发重要的角色,并最终引导了第三次科技革命,带来了人类社会的深刻变革。
微分运算的程序实现,是自然科学的持续发展对程序设计所提出的必然要求。在自动微分(automatic differentiation)的框架以外,微分运算的实现主要有手动求导(manual differentiation)、数值微分(numeric differentiation)及符号微分(symbolic differentiation)三种。出于知识的完整性,本章将首先简单回顾求导的概念,随后对手动求导、数值微分和符号微分分别进行介绍,并且提供相应代码的示例及分析。
在本节中,我们将首先简单回顾求导的基本概念,这是可微分编程的数学基础,也是理解本书内容的先决条件。本节中出现的一些符号,例如函数集





计算机通过0和1的组合表示数字,通过机器指令的组合构造函数,如果我们用



[1] 就理论上而言,我们总可以增加存储的空间来提高所表示数字的精度。在所需的精度范围内,该论断一般而言总是可以成立的。
在式





 注
注
之所以采用








如果两个函数


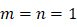

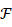
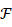
从严格意义上来说,


如果该极限存在,则认为函数

[2] 这里的操作在物理学中也被称作一个算符,这和后文的计算机科学中的运算符(operator)是有区别的。例如对于表达式

从几何上来说,




图1.1 函数导数计算的示意图,式
有时我们也将偏导数简记作




如果对于任意的




应该指出的是,如果我们将求导 (包括偏导数) 这样的操作视为一个由程序所定义的操作


在介绍求导的具体实现方式以前,我们先简单回顾一些求导操作的常见变式。如同上文所指出的那样,一个求导的操作应该被视作一个从函数的集合


梯度操作



从几何的角度来看,












而从程序实现的角度来看,它等价于对多元函数同时进行了


如果说,梯度操作












[3] 读者甚至可以由此联想黎曼几何的一些内容:在黎曼几何之中,我们可以用

我们可以认为,在表达式






上面的







矩阵
符号“


如果我们单看矩阵的某一列(例如第


黑塞矩阵


如果我们将上式带入雅可比矩阵的定义式,就可以得到:
矩阵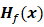
容易看出,这是一个实对称矩阵。数学物理中十分常见的拉普拉斯算符 
如果将式
在对函数和求导运算有了一些基本的了解后,我们将在本章剩余的篇幅中着重介绍在自动微分框架提出之前,微分运算其他的三种实现方式。
手动求导(manual differentiation),顾名思义,就是显式地写出目标函数的导函数。例如,我们来看基于
代码示例1.1 手动求导
from math import sin, cos
def f(x):
return sin(x)
def grad_f(x):
return cos(x) 这样的求导实现方式,从理论上来说不会引入额外的计算误差,同时程序的运行速度可以得到充分的保证。不过这种求导实现方式的缺点也是显而易见的:它过度依赖于人工手动的推导,当函数形式较为复杂时,在公式的推导以及程序的写入过程中很容易产生各种各样的错误,写好的代码很难进行扩展和复用,修改极为不便。
从历史的角度来看,在一些特殊的库(例如


相较于手动求导,数值微分的程序实现显得极为简洁。在本节中,我们将首先介绍数值微分的理论基础,再以此为例对计算问题中的两种误差来源做一个简单的回顾;随后,我们将基于数值微分实现一个自己的grad函数,它能够递归地实现任意阶导数的计算。在本节的最后,我们将对数值微分的时间复杂度进行简单的分析。
数值微分是继手动求导之后又一种微分的程序实现方式,它从求导操作的定义出发,其基本思想可以说相当直观。注意,对于
其中







它自然应该满足:
回顾柯西对于函数极限的表述,对于







我们令函数极限表达式中的








但实际而言,由计算机本身的运算带来的误差,将在两个相近大数相减时变得不可忽略,因此表达式
 注
注
这里的























数值微分的程序实现为我们提供了一个绝佳的实际场景,可向我们展示在使用计算机解决具体问题时两个误差的来源。
舍入误差(round-off error)是由计算机运算本身所造成的误差。一如前文所指出的那样,“计算机通过0和1的组合表示数字,通过机器指令的组合构造函数”,这势必意味着,无论是在计算机上表示数字,还是构造函数,都可能有人为误差的引入。从本质上来说,我们在经典计算机中能够进行的所有存储及运算的操作,仅仅只是对数字和函数这些抽象数学概念的一种物理表述,而这种表述由于其本身的离散性,注定无法做到“完全的精确”[4]。
[4] 做一个类比,如果数字和函数这些抽象的概念是通信领域的模拟电路(analog electronics),那么计算机对这些抽象概念的具体实现则更多体现了数字电路(digital electronics)的构造思路。例如,我们用一定的采样频率对原本在空间上连续的声音和图像进行编码,得到一系列离散的数据。尽管这种编码方式损失了一部分信息,但能够让我们更加方便地对信息进行处理。同样的道理,尽管计算机无法做到对一些数学概念的完美复现,但在绝大多数情况下,现有的物理实现在无数实际的应用中确实被证明行之有效。
如果我们用



在一些情况之下,即使一些数值恰好能被计算机“精确”地表示,这样的表示其实依然不是“完全的”。例如,在一般情况下[5],计算机中的64位浮点数(double)会以







[5] 对于特殊的情况,我们可以参考表1.1。
表1.1
| |
|
|
表达式的值 |
|
| |
任意 |
|
任意 |
|
| 任意 |
|
非零 |
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| 任意 |
|
非零 |
NaN |
另外,我们可以将机器精度(machine accuracy)

在这样的定义之下,我们对64位浮点数(double)的机器误差进行测试,得到

截断误差(truncation error)是计算之中另一类常见的误差来源。如果说舍入误差是由计算机本身硬件的特性所导致,那么截断误差则来自于程序或者算法本身。由于计算机无法处理连续或者趋于无穷(无穷大/无穷小)的变量,我们常常需要设计算法来将连续的变量离散化。例如,在处理数值积分问题时,我们只能对有限多个点进行加权求和,以逼近积分实际的数值。在以有限的积分网格估计无穷且连续的求和时,由于网格选取不够密集或者积分半径不够大所导致的误差,就属于截断误差的范畴。这样的误差完全由算法本身的设计所导致,与计算机硬件运算的精度无关。
数值微分问题与数值积分的情况相似,因为我们使用了含有步长






[6] 在这里,函数可导已经暗含左极限等于右极限的条件,因此在
在





[7] 在英文文献中,式

让我们来考虑一个具体的例子。例如,我们希望采用数值微分的方法,计算函数





代码示例







代码示例1.2 数值微分的误差估计
# 库的引入
import math
import numpy as np
import matplotlib.pyplot as plt
from typing import Callable
# 函数的定义
def f(x):
return x ** 0.5
def err(h, x0, fun: Callable, fun_prime: Callable):
# h为步长;x0为计算导数的点;fcn为待求导的函数;fcn_prime为函数的导函数
return abs((fun(x0+h) - fun(x0)) / h - fun_prime(x0))
# 步长的取值
## 从10^-17 到 10^-1 (对指数)等间距取49个点(包括首尾)
h_list = np.logspace(-17, -1, 49).tolist()
# 参数的设置
x = 0.1
fun = math.sin
fun_prime = math.cos
# 误差的计算
h_log_math = []
err_log_math = []
for h in h_list:
h_log_math.append(math.log10(h))
err_log_math.append(math.log10(err(h,x,fun,fun_prime)))
# 可视化输出
plt.plot(h_log_math, err_log_math, label = "float")
plt.legend(loc = "lower right")
plt.xlabel("log(h)")
plt.ylabel("log(err)")
plt.grid()
plt.savefig(fname = "math_err") # 保存图片
plt.show() 上述程序得到的结果如图







另外,在本书配套的代码中,给出了不同的




图1.2 代码示例1.2程序输出
图1.3 不同的Python库给出的误差曲线比较
如果假定被求导函数



grad函数,这里的grad输入一个待求导的函数fun,返回fun函数的导函数:
from typing import Callable
# 定义函数grad, 用于求输入函数fun的导函数
def grad(fun: Callable, step_size=1E-5)-> Callable:
def grad_f(x):
return (fun(x + step_size) - fun(x)) / step_size
return grad_f 以这样的方式来定义导数,我们就可以通过递归获得函数的任意阶导数,例如:
# 测试
import math
f = math.sin
df = grad(f)
ddf = grad(df)
dddf = grad(ddf)
print(df(0.)) # 返回:0.9999999999833332
print(ddf(0.)) # 返回:-1.000000082740371e-05
print(dddf(0.)) # 返回:-0.999996752071297 如同前文指出的那样,通过数值微分获得的导数的值存在一定的误差,运算的复杂度将随着导数的阶数
有时,我们在获得导函数的同时,还需要知道原本函数的值。因此,我们也常常需要用到下述代码中的value_and_grad函数。注意,尽管这样构造的函数能够多返回一个函数本身的数值,但它并不会为程序引入额外的计算量——即使我们只需要用到函数的导数,运算过程中也同样需要计算函数在待求导处的数值。
# 定义函数value_and_grad,它将会同时计算输入函数grad的值和导函数
def value_and_grad(fun: Callable, step_size=1E-5)-> Callable:
def value_and_grad_f(x):
value = fun(x)
grad = (fun(x + step_size) - value) / step_size
return value, grad
return value_and_grad_f 通过对上述代码进行整理,并且加入一定的注释和类型检查,我们在代码示例1.3中重新给出了数值微分的程序实现。相较而言,它显得更加标准而规范。[8]
[8] 能够熟练地阅读并书写标准化的

grad和value_and_grad相应的实现几乎完全对应。读者在参考了这个基于数值微分的代码实现,并且阅读完后续相关章节之后,甚至可以自己尝试阅读
代码示例1.3 简单函数
import math
from typing import Callable
def value_and_grad(fun: Callable, step_size=1E-5)-> Callable:
'''
构造一个方程,它能够同时计算函数fun的值和它的导数
fun: 被微分的函数,它的输入和返回值需要为一个数(而非数组);
step_size: 数值微分所特有,用于描述微分之中所选取的步长;
返回:
一个和fun具有相同输入结构的函数,这个函数能够同时计算fun的值和它的导函数
'''
def value_and_grad_f(*arg):
# 输入检查
if len(arg) != 1:
raise TypeError(f"函数仅允许有一个变量的输入, 但收到了{len(arg)}个")
x = arg[0]
# 计算函数的值和导函数
value = fun(x)
grad = (fun(x + step_size)- value) / step_size
return value, grad
# 将函数value_and_grad_f返回
return value_and_grad_f
def grad(fun: Callable, step_size=1E-5)-> Callable:
'''
构造一个方程,它仅计算函数fun的导数
fun: 被微分的函数,它的输入和返回值需要为一个数(而非数组);
step_size: 数值微分所特有,用于描述微分之中所选取的步长;
返回:
一个和fun具有相同输入结构的函数,这个函数能够计算函数fun导函数
'''
value_and_grad_f = value_and_grad(fun, step_size)
def grad_f(*arg):
# 仅仅返回导数
_, g = value_and_grad_f(*arg)
return g
# 将函数grad_f返回
return grad_f 利用数值微分,我们同样可以构造具有任意维度输入的函数


grad函数中的参数argnums可以用于指定原函数fun中需要被求偏导的参数的位置。另外,由于我们期待函数fun
has_aux,用于显式地指出函数fun是否存在更多其他的输出;如果其他的输出确实存在,程序将忠实地将它们返回,但仅对第一个输出的数值进行求导。这里参数的定义完全仿照
grad函数的定义,这在4.1.1节中将会被再次提到。
代码示例1.4 任意函数
import numpy as np
from copy import deepcopy
from typing import Callable, Union, Sequence
def value_and_grad(fun: Callable, argnums: Union[int, Sequence[int]] = (0,),
has_aux: bool = False, step_size=1E-5,
)-> Callable:
'''
构造一个方程,它能够同时计算函数fun的值和它的梯度
fun: 被微分的函数,需要被微分的位置由参数argnums指定,
而函数fun返回的第一个值需要为一个数(而非数组),
如果函数fun有另外的输出, 则需令has_aux参数为True;
argnums: 可选参数,可以为整数int或者一个整数的序列, 用于指定微分的对象;
has_aux: 可选参数,bool类型,用于显式地声明函数fun是否存在除整数以外的输出;
step_size: 数值微分所特有,用于描述微分之中所选取的步长;
返回:
一个和fun具有相同输入结构的函数,这个函数能够同时计算fun的值和指定位置的导函数
'''
if isinstance(argnums, int):
argnums = (argnums,)
def value_and_grad_f(*args):
# 输入检查
max_argnum = argnums if isinstance(argnums, int) else max(argnums)
if max_argnum >= len(args):
raise TypeError(f"对参数 argnums = {argnums}微分需要至少 "
f"{max_argnum+1}个位置的参数作为变量被传入,"
f"但只收到了{len(args)}个参数")
# 构造计算导函数所需的输入
diff_arg_list = []
for num in argnums:
temp_args = deepcopy(list(args))
temp_args[num] += step_size * np.ones_like(args[num], dtype=np.float64)
diff_arg_list.append(temp_args)
# 计算函数的值和导函数
if not has_aux:
value = fun(*args)
g = [(fun(*diff_args)-value)/ step_size for diff_args in diff_arg_list]
else:
value, aux = fun(*args)
g=[(fun(*diff_args)[0]-value)/step_size for diff_args in diff_arg_list]
# 程序输出
g = g[0] if len(argnums)==1 else tuple(g)
if not has_aux:
return value, g
else:
return (value, aux), g
return value_and_grad_f
def grad(fun: Callable, argnums: Union[int, Sequence[int]] = (0,),
has_aux: bool = False, step_size=1E-5,
)-> Callable:
'''
构造一个方程,它仅计算函数fun的梯度
fun: 被微分的函数,需要被微分的位置由参数argnums指定,
而函数fun返回的第一个值需要为一个数(而非数组),
如果函数fun有另外的输出, 则需令has_aux参数为True;
argnums: 可选参数,可以为整数int或者一个整数的序列, 用于指定微分的对象;
has_aux: 可选参数,bool类型,用于显式地声明函数fun是否存在除整数以外的输出;
step_size: 数值微分所特有,用于描述微分之中所选取的步长;
返回:
一个和fun具有相同输入结构的函数,这个函数能够计算函数fun的梯度
'''
value_and_grad_f = value_and_grad(fun=fun, argnums=argnums,
has_aux=has_aux, step_size=step_size)
def grad_f(*arg):
# 仅仅返回导数
_, g = value_and_grad_f(*arg)
return g
def grad_f_aux(*arg):
# 返回导数,以及原函数输出的其他结果
(_, aux), g = value_and_grad_f(*arg)
return g, aux
return grad_f_aux if has_aux else grad_f 读者可以略过以上代码,直接来看一个基于以上代码的程序测试示例如下:
def f(x,y):
aux = "function called"
return np.sin(x+2*y), aux
x = np.array([0.,0.,np.pi])
y = np.array([0.,np.pi,0.])
df1 = grad(f, argnums=0, step_size=1E-5, has_aux=True) # f对第1个参数的偏导
df2 = grad(f, argnums=1, step_size=1E-5, has_aux=True) # f对第2个参数的偏导
df12 = grad(f, argnums=(0,1), step_size=1E-5, has_aux=True) # f 的全微分(梯度)
print(f(x,y))
print(df1 (x,y))
print(df2 (x,y))
print(df12(x,y))
'''
程序输出:
>> (array([ 0.0000000e+00, -2.4492936e-16, 1.2246468e-16]), 'function called')
>> (array([ 1., 1., -1.]), 'function called')
>> (array([ 2., 2., -2.]), 'function called')
>> ((array([ 1., 1., -1.]), array([ 2., 2., -2.])), 'function called')
''' 正是由于

argnums=(0,1)时,程序输入与输出的数组形状相同,这相当于一个梯度操作


另外,关于数值微分的最后一点说明是,由于对函数





[9] 比如,在深度学习领域,有时我们需要对神经网络当中上百万个甚至上亿个参数进行优化,这相当于令我们的函数



尽管如此,由于其本身简单的实现原理以及方便的程序实现方式,数值微分方法至今依然在许多不同的领域发挥着重要的作用。
截断误差的存在以及一些情况下无法被接受的计算复杂度,使得数值微分方法具有其自身的局限。为了彻底消除数值微分中的截断误差,计算图的概念将在本节的开始被自然地引入,它在符号微分及第2章的自动微分中拥有举足轻重的地位。在本节中,我们还将给出一个符号微分的代码示例,并基于此再次实现一个可用的grad函数:代码示例

从符号微分开始,计算图(computational graph)的概念扮演起愈发重要的角色。如果说数值微分程序的正确实现依赖于对“求导”这一概念的本质理解,那么符号微分的程序实现则依赖于对“计算”这一概念的重新审视。加减乘除、指数对数、三角函数、特殊函数……人类对于其中的每一个运算的优先级和表达方式,都有符号体系上基于经验的约定。但是,这样的约定对于机器层面的运行而言,往往是不够高效的。例如,我们考虑如下这个二元函数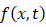
在这里[10],尽管人类可以一眼看出这个公式所提示的运算顺序,但如果我们期待直接从公式出发,将类似这样的表达式直接翻译成机器语言供计算机执行,则往往是困难且难于实现的。不过,如果我们针对上述公式构造出如图1.4所示的树形结构的计算图,就可以让程序清晰地理解函数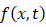
[10] 这里的

图1.4 公式
读者应该不难看出图






还应该注意的是,计算图1.4中的所有数字(例如图中的“1”和“2”)或者变量(例如图中的“





但是,计算图的作用远远不止为我们提供一个节点处的数值那么简单。事实上,通过为每一个节点赋予各种不同的运算操作,我们可以递归地实现诸如表达式的打印、求导、展开、化简等不同的任务。在编译原理中,可以通过计算图的构建,实现中缀表达式(infix expression)和前缀表达式(prefix expression)、后缀表达式(suffix expression)之间的相互转化[11]。而在一些更加复杂的例子中,利用计算图构建出的不同公式甚至被用于符号回归(symbolic regression),对公式进行拟合。麻省理工学院的Max Tegmark教授及其合作者,在2020年发表的一篇名为AI Feynman: a Physics-Inspired Method for Symbolic Regression的文章中,利用计算图进行了表达式的构造,同时结合量纲分析、多项式拟合、神经网络、对称性分析等不同的研究手段,使得计算机能够通过极为有限的数据,自动发现待拟合函数最为合理的符号表达式,从而极大推动了符号回归领域相关算法的发展。
[11] 例如,对于一个中缀表达式


在接下来的篇幅之中,我们将着重展示如何通过构建计算图,实现表达式的求值、打印及微分的运算,并通过相应的示例代码,令读者获得对符号微分的深刻认识。随后,我们将通过调用


应该指出的是,计算图在符号微分和自动微分中所扮演的地位是本质性的。
在进一步讨论计算图具体代码的实现之前,我们强烈建议读者首先阅读附录A中对

__init__和__new__函数、__str__和__repr__函数之间的联系与区别,而这些在符号微分的程序实现之中恰好将被反复地使用。另外,为了能够更好地理解本节的内容,我们希望读者熟悉算符重载的相应语法,相应的介绍同样在附录
通常而言,无论是对于有向图还是无向图,我们都可以采用类似代码示例

代码示例
Expr,本节中出现的所有其他类都需要从该类继承。
代码示例1.5.1 符号微分的简单实现(Expr类)
class Expr(object):
_operand_name = None
def __init__(self, *args):
for arg in args:
if isinstance(arg, (int, float)):
arg = Variable(str(arg))
self._args = args
""" 测试 """
# print([str(item) for item in args], self._operand_name)
# 加法
def __add__(self, other):
return Add(self, other)
def __radd__(self, other):
return Add(other, self)
# 减法
def __sub__(self, other):
return Sub(self, other)
def __rsub__(self, other):
return Sub(other, self)
# 乘法
def __mul__(self, other):
return Mul(self, other)
def __rmul__(self, other):
return Mul(other, self)
# 除法
def __truediv__(self, other):
return Div(self, other)
def __rtruediv__(self, other):
return Div(other, self)
# 乘方
def __pow__(self, other):
return Pow(self, other)
def __rpow__(self, other):
return Pow(other, self)
def __str__(self):
terms = [str(item) for item in self._args]
operand = self._operand_name
return "({})".format(operand.join(terms))上面式子之中出现的Add、Sub、Mul、Div及Pow,都是继承自Expr类的名称,它们的定义将会在后面给出。需要指出的是,Expr类已经在形式上完成了所有(可微的)算数运算符的重载。在计算图构建完成之后,__str__方法则可以递归地实现表达式的打印。接下来,我们首先给出叶子节点Variable类的定义,它被用作处理函数的输入,如代码示例1.5.2所示。
代码示例1.5.2 符号微分的简单实现(Variable类)
VARIABLE_NAME = "Variable"
class Variable(Expr):
_operand_name = VARIABLE_NAME
__slots__ = ("name",)
def __init__(self, name: str):
""" 构造函数 """
try:
assert(isinstance(name, str))
except:
raise TypeError("name parameters should be string, \
get type {} instead".format(type(name)))
finally:
self.name = name
def __str__(self):
return self.name
def diff(self, var):
if self.name == var.name:
return One()
else:
return Zero() 上述的Variable类作为叶子节点,将是所有表达式打印操作__str__及微分操作diff的递归终点。这里,diff函数接受的参数var代表求导的对象,它所返回的One()和Zero()分别是由Expr类构造的代表变量

One和Zero的定义。
[12] 参考附录

代码示例1.5.3 符号微分的简单实现(Zero和One的单例)
""" 数字0的单例 """
class Zero(Expr):
_instance = None
def __new__(cls, *args):
if Zero._instance == None:
obj = object.__new__(cls)
obj.name = "0"
return obj
else:
return Zero._instance
def __str__(self):
return "0"
""" 数字1的单例 """
class One(Expr):
_instance = None
def __new__(cls, *args):
if One._instance == None:
obj = object.__new__(cls)
obj.name = "1"
return obj
else:
return One._instance
def __str__(self):
return "1" 对于位于计算图中间的表达式节点,也就是Add、Sub、Mul、Div及Pow函数的实现,将在下面的代码示例中分别给出。例如,对于加法节点Add的表达式打印操作,由于Add类继承自Expr,只需要指定参数_operand_name为“+”,程序即可自动调用位于Expr类中的__str__函数,实现表达式的递归打印。
注意,对于微分操作来说,如果我们有加法恒等式:
其中



此后的符号约定与这里一致。代码示例1.5.4给出了Add类的程序实现,注意在Expr类的初始化函数中,所有的输入变量都已经被存储在元组self._args中。
代码示例1.5.4 符号微分的简单实现(Add类)
class Add(Expr):
_operand_name = " + "
def diff(self, var):
terms = self._args
terms_after_diff = [item.diff(var) for item in terms]
return Add(*terms_after_diff) 减法操作与加法类似。注意,self._args的元组类型能够保证输入参数的顺序不变,而这里所有的算符都认为是二操作数的算符,因此列表中虽然出现了循环,但实则只是遍历了减数和被减数两个变量而已。如果有关系式:
那么相应的递归表达式就为:
其程序实现如代码示例1.5.5所示。
代码示例1.5.5 符号微分的简单实现(Sub类)
class Sub(Expr):
_operand_name = " - "
def diff(self, var):
terms = self._args
terms_after_diff = [item.diff(var) for item in terms]
return Sub(*terms_after_diff) 同样地,对于乘法操作:
我们可以得到相应的用于求导的递归表达式:
这个函数表达式的内涵是极为深刻的:在一些数学理论中,表达式1.28的地位常常是根本性的。另外,由于在求导操作作用于乘法时,表达式的长度将显著地增长(实际上,对于其他操作也是如此),因此在递归深度较大时,如果不进行化简[13],我们常常会面临表达式长度的指数膨胀(expression swell)——这也是符号微分在实际场景中所面临的困境之一。
[13] 实际上,在绝大多数情况下,解析的表达式(如果真的存在的话)往往确实无法被有效地化简。
乘法操作的代码实现如代码示例1.5.6所示。
代码示例1.5.6 符号微分的简单实现(Mul类)
class Mul(Expr):
_operand_name = " * "
def diff(self, var):
terms = self._args
if len(terms) != 2:
raise ValueError("Mul operation takes only 2 parameters")
terms_after_diff = [item.diff(var) for item in terms]
return Add(*terms_after_diff) 对于除法操作:
我们可以得到相应的用于求导的递归表达式:
当然,出于礼貌,我们在代码示例1.5.7中加上了对除数和被除数是否为常数的判断,象征性地化简了一下最终的表达式,让读者能够对表达式的化简过程形成一些大致的感觉。
代码示例1.5.7 符号微分的简单实现(Div类)
class Div(Expr):
_operand_name = " / "
def diff(self, var):
numer = self._args[0] # 分子(被除数) numerator
denom = self._args[1] # 分母(除数) denomenator
d_numer = numer.diff(var)
d_denom = denom.diff(var)
if isinstance(numer, (int, float, np.ndarray)):
# 如果分子是常数
return Zero() - d_denom * numer / denom ** 2
elif isinstance(denom, (int, float, np.ndarray)):
# 如果分母是常数
return d_numer / denom
else:
return d_numer / denom - d_denom * numer / denom ** 2 最后是对乘方的运算。假如:
我们可以得到相应的用于求导的递归表达式:
如不加说明,对数符号log默认以自然对数e为底。不过,直接调用这样的表达式往往对应着较大的计算开销。实际工程中的做法是将以上表达式进行略微变形:
这相当于对等式的两边同时取对数后再求导,由于
代码示例1.5.8 符号微分的简单实现(Pow类)
class Pow(Expr):
_operand_name = " ** "
def diff(self, var):
base = self._args[0] # 底数
pow = self._args[1] # 幂
dbase = base.diff(var)
dpow = pow.diff(var)
if isinstance(base, (int, float, np.ndarray)):
return self * dpow * Log(base)
elif isinstance(pow, (int, float, np.ndarray)):
return self * dbase * pow / base
else:
return self * (dpow * Log(base) + dbase * pow / base) 这里由于用到了对数操作,我们还需要构造对数运算Log的节点,注意到:
(1.33)
我们不难得到Log类的程序实现,如代码示例1.5.9所示。
代码示例1.5.9 符号微分的简单实现(Log类)
class Log(Expr):
def __str__(self):
return f"log({str(self._args[0])})"
def diff(self, var):
return self._args[0].diff(var) / self._args[0] 通过对数算符Log节点的构造,我们期待读者能够对自定义算符的过程产生初步的印象。这样的过程常常被用在对代码的加速中,或者在一些更加专业的领域中用于处理一些特殊函数,抑或是用于解决一些因为数值不稳定而带来的问题。
一个应该注意的细节是,在实际的工程中,如果需要将以上不同类的代码分在不同的文件中,那么对于Expr类所在的文件,Add、Mul等算符类的import操作需要置于文件的底端,不然这将导致程序因为文件的循环引用而报错。
最终,我们可以在程序的外围简单地定义diff函数,如代码示例1.5.10所示。
代码示例1.5.10 符号微分的简单实现(diff函数)
def diff(function, var):
return function.diff(var) 或者,使用一些特殊的编程技巧,我们也可以在形式上构造出类似于
grad函数——尽管这样定义的函数基本上很难有什么实际的用途。
代码示例1.5.11 符号微分的简单实现(grad函数)
def grad(fun, argnum = 0):
'''''
构造一个方程,它仅计算函数fun的梯度
fun: 被微分的函数,需要被微分的位置由参数argnum指定, 函数的返回只能为一个数
argnum: 可选参数,只能为整数, 用于指定微分的对象;若不指定则默认对第一个参数求导
返回:
一个和fun具有相同输入结构的函数,这个函数能够计算函数fun的梯度
'''
def grad_f(*args):
namespace = []
for i in range(len(args)):
namespace.append("arg" + str(i))
varlist = [Variable(name) for name in namespace]
expr = str(diff(fun(*varlist), varlist[argnum]))
for i in range(len(args)):
exec("{} = {}".format(namespace[i], args[i]))
return eval(expr)
return grad_f 我们在代码示例1.5.12中给出了对符号微分程序实现的测试示例。
代码示例1.5.12 符号微分的简单实现(测试示例)
x = Variable("x")
y = Variable("y")
def f(x,y):
return x + y**x
expr = str(diff(f(x,y), x))
print(expr)
>> (1 + ((y ** x) * ((1 * log(y)) + ((0 * x) / y))))
df = grad(f)
print(df(1.0, 2.0))
>> 2.386294361119891 这里生成的表达式“(1 + ((y ** x) * ((1 * log(y)) + ((0 * x) / y))))”,是可以直接被复制粘贴到程序中执行的,这也是在grad函数中可以直接调用
eval函数的原因。
以上符号微分的代码实现完全参考自


在实际的科研中,我们常常需要计算一些多项式的显式表达式。例如,在量子力学中,在谐振子势能
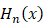


(1.34)
这里的
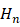
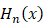

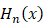
[14] 主量子数、角量子数、磁量子数和自旋量子数的概念不止对应着原子核

[15] 在概率论中,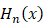

(1.35)
为了得到

diff函数,其具体的程序实现如代码示例1.6所示。
代码示例1.6 符号微分与厄米多项式
import math
from sympy import symbols, simplify, expand, diff
e = math.e
x = symbols("x")
# 计算厄米多项式的表达式
def H_expr(order: int):
assert isinstance(order, int) and order >= 0
expr = e ** (-x**2)
for _ in range(order):
expr = diff(expr, x)
expr *= e ** (x**2) * (-1) ** order
return expand(simplify(expr))
# 对前15个表达式进行打印
for i in range(15):
print("H{:<2.0f}(x) = {}".format(i, H_expr(i)))
# 一个可以直接调用的厄米多项式函数
def H(x, n):
""" 计算Hn(x) """
return eval(str(H_expr(n))) 在这里,程序书写的过程完全对应于翻译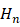

symbols函数的调用,等价于代码示例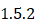
Variable类的构造,而这里的diff函数与我们自己定义的diff函数用法完全相同。通过调用
simplify函数,我们实现了表达式的化简(例如消去所有冗余的
expand函数,程序可以自动将多项式中的项按照次数从高到低进行排列,十分方便。
这里打印出程序的一部分返回值,供大家参考。
H0 (x) = 1
H1 (x) = 2.0*x
H2 (x) = 4.0*x**2 - 2.0
H3 (x) = 8.0*x**3 - 12.0*x
H4 (x) = 16.0*x**4 - 48.0*x**2 + 12.0
H5 (x) = 32.0*x**5 - 160.0*x**3 + 120.0*x
H6 (x) = 64.0*x**6 - 480.0*x**4 + 720.0*x**2 - 120.0
H7 (x) = 128.0*x**7 - 1344.0*x**5 + 3360.0*x**3 - 1680.0*x
H8 (x) = 256.0*x**8 - 3584.0*x**6 + 13440.0*x**4 - 13440.0*x**2 + 1680.0
H9 (x) = 512.0*x**9 - 9216.0*x**7 + 48384.0*x**5 - 80640.0*x**3 + 30240.0*x
… 大家可以将它与表1.2中的参考值进行对照。
表1.2 前6个概率论和物理学中的埃尔米特多项式
| 序号 |
概率论 |
物理学 |
|---|---|---|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
当然,


(1.36)
这里的归一化系数


(1.37)
循环边界条件下
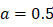




代码示例1.7 符号积分与跃迁振幅
import math
from sympy import symbols, Matrix, simplify, expand ,
integrate, exp, oo, print_latex
# A = Matrix([[9, -4, 0, 0, 0, 0, 0, -4],
# [-4, 9, -4, 0, 0, 0, 0, 0],
# [0, -4, 9, -4, 0, 0, 0, 0],
# [0, 0, -4, 9, -4, 0, 0, 0],
# [0, 0, 0, -4, 9, -4, 0, 0],
# [0, 0, 0, 0, -4, 9, -4, 0],
# [0, 0, 0, 0, 0, -4, 9, -4],
# [-4, 0, 0, 0, 0, 0, -4, 9]]) / 4
#
# u = Matrix([[x0, x1, x2, x3, x4, x5, x6, x7 ]])
# S = simplify(u * A * u.T)
# print(S)
x0, x1, x2, x3, x4, x5, x6, x7 = symbols("x0, x1, x2, x3, x4, x5, x6, x7")
S = x0*(9*x0/4 - x1 - x7) + x1*(-x0 + 9*x1/4 - x2) + \
x2*(-x1 + 9*x2/4 - x3) + x3*(-x2 + 9*x3/4 - x4) + \
x4*(-x3 + 9*x4/4 - x5) + x5*(-x4 + 9*x5/4 - x6) + \
x6*(-x5 + 9*x6/4 - x7) + x7 * (-x0 - x6 + 9*x7/4)
S = expand(S)
print(S)
f = exp(-S)
for x in [x1, x2, x3, x4, x5, x6, x7]:
f = simplify(expand(integrate(f, (x, -oo, +oo))))
print(f)
print_latex(f)在代码示例1.7中,注释部分可以用于生成关于作用量
integrate函数进行积分的计算,并在每次积分过后进行表达式的化简。在性能一般的计算机上运行上述代码需要花费一定的时间,不过最终可以打印出积分结果的符号表达式与
积分最终结果的符号表达式为:
➢ 128*sqrt(1889)*pi**(7/2)*exp(-7497*x0**2/7556)/39669

➢ \frac{128 \sqrt{1889} \pi^{\frac{7}{2}} e^{- \frac{7497 x_{0}^{2}} {7556}}}{39669}
两者对应着同样的解析表达式:
这意味着,



不过,符号微分的实现对程序框架的设计提出了过高的要求:所有的表达式必须是“闭合的”。例如,
 注
注
本节所举的两个例子是存在内在联系的。在物理学中,我们可以证明如下近似关系:
其中,


需要说明的是,这里的






我们可以用积分的结果来对上述关系进行验证。为此,我们注意到:
正因如此,我们能够使用高维积分的方式测量体系基态的能量(尽管这种积分通常由量子蒙特卡罗方法完成)。
读者服务:
微信扫码关注【异步社区】微信公众号,回复“e60935”获取本书配套资源以及异步社区15天VIP会员卡,近千本电子书免费畅读。
在第1章中,我们首先对求导的概念进行了简单的回顾,随后介绍了在自动微分的框架以外,微分运算的其他三种实现方式。其中,手动求导充分保证了程序运行的速度和性能,但以此为基础的程序实现由于过度依赖人工的推导,代码难以扩展和复用。数值微分的程序实现相较于手动求导显然更加便捷,它可以使我们快速获得对函数在一个邻域中变化趋势的直观印象;不过,截断误差的存在以及一些情况下难以被接受的计算复杂度,使得数值微分方法具有其自身的局限。从符号微分开始,计算图的概念被自然地引入,尽管精确的计算流程从理论上彻底消除了截断误差,但对表达式闭合[1]的要求以及表达式长度的急剧膨胀,成为符号微分在实际场景之中所面临的困境。
[1] 闭合表达式(closed-form expression)在数学上有其另外的内涵,但从计算的角度出发,闭合表达式要求计算图内部的节点不得参与到条件语句(

在这一章中,我们将开始着重介绍自动微分(Automatic Differentiation)的有关概念,它将作为一种基本的数据结构,贯穿后续所有的章节。自动微分和符号求导有诸多相似之处:它们同样依赖于计算图的构建,同样依赖于求导的递归实现。从某种意义上来说,它们甚至拥有完全相同的数据结构。不过,二者的区别也是显著的:符号微分侧重于符号,而自动微分则侧重于数值。从包含关系上来说,数值是一种特殊的符号——初识数学的人往往是先学会计算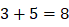

《庄子•达生》中有言:“用志不分,乃凝于神。”自动微分作为一种专门化的计算图网络,通过在计算的过程中同时完成计算图的构建及具体数值的带入,克服了符号微分中表达式长度急剧膨胀的问题,也放松了“符号表达式应该闭合”这一要求。尽管在本章之后的
从自动微分的具体实现方案来看,它又分为前向模式(forward mode)和反向模式(backward mode)两种算法。在本章中,我们将对这两种依赖于相同网络结构的不同算法分别进行介绍,从中体会自动微分库自上而下的结构设计。
本节将首先对自动微分前向模式的理论部分做一个简单的介绍,令读者首先把握前向模式的主要思想。在此基础之上,我们将通过二元数的相关理论,对前向模式进行更进一步的诠释,严格地论证将微分算符

grad函数能够进行一阶导数的计算。
 注
注
跳过
前向模式的理论相对于反向模式而言显得较为简单。我们注意到,对于一个


[2] 如果不加说明,我们假设本章中所有的函数都至少是一阶可微的。
将上式写成分量形式,它等价于:
 注
注
通常而言,我们也可以将式
写作
这样的记号在一些情况下是有好处的:符号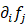

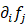

之中的


式











从计算图的视角来审视以上的微分运算,











如果我们为计算图的任意节点
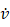





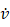

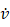





实际上,如果我们将



式
这告诉我们,链式求导法则对应着雅可比矩阵的相乘。作为记号的改变,我们还可以将式
注意,本节中出现的所有矩阵,正对应着式

正因如此,由前向模式所定义的函数在
jvp函数,它代表着雅可比-矢量乘法(Jacobian-Vector Product)。采取jvp这样的称呼或许是有其历史原因的:在


y=f.forward(x)从效果上来看完全等价于y=f(x);在这里,名称forward仅用于指示运算操作在计算图中传播的方向,而非自动微分的前向模式。正因如此,

jvp,作为前向模式计算时函数的名称。
此外还应该指出的是,矢量







也就是说,在



这告诉我们,每一次前向传播,我们可以求出雅可比矩阵的一列。由于雅可比矩阵的列数由函数

作为一个例子,考虑式

图2.1 (左)式
| 主值 |
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 切值 |
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
计算图的构建过程以及前向微分的程序实现将在
[3] 参考文献:Baydin A G, Pearlmutter B A, Radul A A, et al. Automatic differentiation in machine learning: a survey[J]. Journal of machine learning research, 2018, 18. (本节内容与该篇文献相比显得详细许多)
雅可比矩阵与数对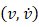
从数学的角度来看,我们可以将自动微分的前向模式理解为将函数延拓到二元数域的结果。它可以被视作对函数泰勒展开的一种截断:
其中


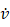

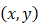
这里的





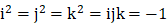


对于二元数来说,我们以如下方式定义加法和乘法:
取反操作作用于二元数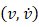

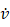
我们不难由此定义出减法。读者可以在
对于除法,我们有:
这可以从关系 
解决了四则运算。接下来让我们来考察乘方运算,在底数为自然常数
如果我们期待二元数同样能够满足这样的定义,则将有:
对数运算是乘方运算的逆运算,如果我们期待:
则应该有:
稍加对比,我们不难得到

当然,对于其他任意阶可微的光滑函数
在式
 注
注
前文提到,式


可以证明,函数






以下是式
式


这样,如果我们将式


由于通常来说上式对任意的

考虑到关系
式

例如,如果


另外一个常见的例子是取
下面我们重新对多元函数






我们将



也即是说
这是对式



在


式









从本质上来说,二元数幂零元


前向微分的程序实现和符号求导类似,同样需要用到运算符的重载。以加法和乘法的算符前向传播为例,如果不加入任何的类型检查,我们甚至只需要定义一个Variable类,即可完成所有的任务。
代码示例2.1 自动微分前向模式的简单实现(加法、乘法)
class Variable(object):
def __init__(self, value, dot=0.):
self.value = value
self.dot = dot
# 加法的重载
def __add__(self, other):
res = Variable(self.value + other.value)
res.dot = self.dot + other.dot
return res
def __radd__(self, other):
return self.__add__(other)
# 乘法的重载
def __mul__(self, other):
res = Variable(self.value * other.value)
res.dot = other.value * self.dot + self.value * other.dot
return res
def __rmul__(self, other):
return self.__mul__(other) 我们在附录





当然,如果我们尝试将代码变得更加专业实用,可以考虑在程序中加入对叶节点的判断以及输入类型的转换,具体的程序实现如代码示例2.2.1所示。
代码示例2.2.1 自动微分前向模式的算法实现(初始化、类型判断)
import math
from typing import Callable, List
class Variable(object):
_is_leaf = True
def __init__(self, value, dot=0):
self.value = value
self.dot = dot
@staticmethod
def to_variable(obj):
if isinstance(obj, Variable):
return obj
try:
return Variable(obj)
except:
raise TypeError("Object {} is of type {}, which can not be interpreted"
"as Variables".format(type(obj).__name__, type(obj))) 代码示例2.2.2中关于加法和乘法算符的重载与代码示例2.1完全类似。
代码示例2.2.2 自动微分前向模式的算法实现(重载加法与乘法算符)
# 加法的重载
def __add__(self, other):
""" self + other """
if not isinstance(other, Variable):
other = self.to_variable(other)
res = self.to_variable(self.value + other.value)
res.dot = self.dot + other.dot
res._is_leaf = False
return res
def __radd__(self, other):
""" other + self """
return self.__add__(other)
# 乘法的重载
def __mul__(self, other):
""" self * other"""
if not isinstance(other, Variable):
other = self.to_variable(other)
res = self.to_variable(self.value * other.value)
res.dot = other.value * self.dot + self.value * other.dot
res._is_leaf = False
return res
def __rmul__(self, other):
""" other * self """
return self.__mul__(other) 在重载减法算符之前,我们需要首先通过函数__neg__重载取反操作(这和2.1.2节中关于二元数运算规则的讨论顺序是一致的)。代码示例2.2.3与式
代码示例2.2.3 微分前向模式的算法实现(重载取反与减法)
# 取反操作的重载
def __neg__(self):
""" - self """
self.value = - self.value
self.dot = -self.dot
return self
# 减法的重载
def __sub__(self, other):
""" self - other """
if not isinstance(other, Variable):
other = self.to_variable(other)
other = - other # 这里将用到重载的__neg__
return self.__add__(other)
def __rsub__(self, other):
""" other - self """
if not isinstance(other, Variable):
other = self.to_variable(other)
self = -self # 这里将用到重载的 __neg__
return self.__add__(other) 除法算符会稍微复杂一些,它还涉及除零的判断 (类似的问题在符号求导中是不会存在的),代码示例2.2.4与式
代码示例2.2.4 自动微分前向模式的算法实现(重载除法)
# 除法的重载
def __truediv__(self, other):
""" self / other """
if not isinstance(other, Variable):
other = self.to_variable(other)
if other.value == 0:
raise ZeroDivisionError("division by zero")
res = Variable(self.value / other.value)
res.dot = 1. / other.value * self.dot \
- 1 / (other.value ** 2) * self.value * other.dot
res._is_leaf = False
return res
def __rtruediv__(self, other):
""" other / self """
if not isinstance(other, Variable):
other = self.to_variable(other)
if self.value == 0:
raise ZeroDivisionError("division by zero")
res = Variable(other.value / self.value)
res.dot = 1. / self.value * other.dot \
- 1 / (self.value ** 2) * other.value * self.dot
res._is_leaf = False
return res 乘方的操作相对比较复杂,在之前的符号求导中,我们只在乎程序是否能够返回正确的符号表达式,而没有在运算的过程中赋予变量具体的值。但是,在自动微分中,我们需要对乘方的底数(base)和幂(power)的不同取值情况进行更加细致的讨论。
例如,在指数为



__rpow__的重载。具体的程序实现如代码示例2.2.5所示。
[4] 如果读者在










type((-8)**(1/3))”返回的结果是<class 'complex'>。
有关于负数的指数问题,其本质是复数的指数问题, 而在黎曼面上,复变函数
代码示例2.2.5 自动微分前向模式的算法实现(重载乘方)
# 乘方的重载
def __pow__(self, other):
""" self ** other"""
if not isinstance(other, Variable):
other = self.to_variable(other)
# 指数和底数出现0的情况
if other.value == 0 or self.value == 0:
if self.value == 0 and other.value ==0:
raise ValueError("0^0 occurred during calculation.")
elif self.value == 0: # 0^x
res = self.to_variable(0.)
elif other.value == 0: # x^0
res = other.to_variable(1.)
else:
raise ValueError(" This Error should never have occurred.")
# 指数为整数的情况
elif int(other.value) == other.value and other._is_leaf:
res = self.to_variable(self.value ** other.value)
res.dot = other.value * self.value ** (other.value - 1) * self.dot
# 一般情况
else:
if self.value < 0:
raise ValueError("Can't take the power of a negative number currently,
" may be implemented later")
res = self.to_variable(self.value ** other.value)
res.dot = other.value * self.value ** (other.value - 1) * self.dot \
+ self.value ** other.value * math.log(self.value) * other.dot
res._is_leaf = False
return res
def __rpow__(self, other):
""" other ** self """
if not isinstance(other, Variable):
other = self.to_variable(other)
# 指数和底数出现0的情况
if other.value == 0 or self.value == 0:
if self.value == 0 and other.value ==0:
raise ValueError("0^0 occurred during calculation.")
elif other.value == 0: # 0^x
res = self.to_variable(0.)
elif self.value == 0: # x^0
res = other.to_variable(1.)
else:
raise ValueError(" This Error should never have occurred.")
# 一般情况
else:
if other.value < 0:
raise ValueError("Can't take the power of a negative number currently
" may be implemented later")
res = self.to_variable(other.value ** self.value)
res.dot = self.value * other.value ** (self.value - 1) * other.dot \
+ other.value ** self.value * math.log(other.value) * self.dot
res._is_leaf = False
return res 当然,如果我们希望在打印结果时,程序能够返回靠谱一些的结果,只需要简单重写__str__函数即可,如代码示例2.2.6所示。
代码示例2.2.6 自动微分前向模式的算法实现(重写str函数)
def __str__(self):
if isinstance(self.value, Variable):
return str(self.value)
return "Variable({})".format(self.value) 行文至此,我们基本完成了Variable类的书写。如果需要添加Variable类对大小比较的支持,我们可以完全参考附录
当然,Variable类的构造本身仅仅只是手段,我们的最终目的是用前向模式求出函数在某点处的微分。由此定义的value_and_grad函数如示例代码2.3.1所示。
代码示例2.3.1 基于前向模式的value_and_grad函数
def value_and_grad(fun: Callable,
argnum: int = 0,)-> Callable:
'''''
构造一个方程,它能够同时计算函数fun的值和它的梯度
fun: 被微分的函数。需要被微分的位置由参数argnums指定, 函数的返回只能为一个数
argnum: 可选参数,只能为整数, 用于指定微分的对象;不指定则默认对第一个参数求导
返回:
一个和fun具有相同输入结构的函数,这个函数能够同时计算fun的值和指定位置的导函数
'''
def value_and_grad_f(*args):
# 输入检查
if argnum >= len(args):
raise TypeError(f"对参数 argnums = {argnum}微分需要至少 "
f"{argnum+1}个位置的参数作为变量被传入,"
f"但只收到了{len(args)}个参数")
# 构造求导所需的输入
args_new: List[Variable] = []
for arg in args:
if not isinstance(arg, Variable):
arg_new = Variable.to_variable(arg)
arg_new.dot = 0.
else:
arg_new = arg
args_new.append(arg_new)
# 将待求导对象的dot值置为1,其余置为0
args_new[argnum].dot = 1.
# 计算函数的值和导函数
value = fun(*args_new)
g = value.dot
# 程序输出
return value, g
# 将函数value_and_grad_f返回
return value_and_grad_f 简单来说,如果需要求取关于第
Variable类,同时将第
Variable分量的dot参数赋值为1,其余分量dot参数赋值为0即可。有了value_and_grad函数,grad函数即可被方便地构造出来,如代码示例2.3.2所示。
代码示例2.3.2 基于前向模式的grad函数
def grad(fun: Callable,
argnum: int = 0,)-> Callable:
'''''
构造一个方程,它仅计算函数fun的梯度
fun: 被微分的函数。需要被微分的位置由参数argnums指定, 函数的返回只能为一个数
argnum: 可选参数,只能为整数, 用于指定微分的对象;不指定则默认对第一个参数求导
返回:
一个和fun具有相同输入结构的函数,这个函数能够计算函数fun的梯度
'''
value_and_grad_f = value_and_grad(fun=fun, argnum=argnum)
def grad_f(*args):
# 仅仅返回导数
_, g = value_and_grad_f(*args)
return g
return grad_f 作为一个简单的测试,我们来看如代码示例2.3.3所示的测试案例。
代码示例2.3.3 grad函数测试
def f(x,y):
return (x + y) ** 2
x, y = 1.0, 2.0
df1 = grad(f, argnum=0, )
df2 = grad(f, argnum=1, )
""" 第零阶 """
print(f(x,y)) # >> 9.0
""" 第一阶 """
print(df1 (x,y)) # >> 6.0
print(df2 (x,y)) # >> 6.0 通过前向模式的自动微分,我们同样可以完成高阶导数的计算。直觉上的方案是将Variable类中所有dot的值同样转化为Variable类的实例。这样的直觉无疑是准确的,但在实际的代码设计中,该方案需要克服的主要难点在于算符的循环重载问题。在接下来的篇幅中,我们仅仅指出高阶导数的实现将面临的主要问题和可能的解决方案——
一个最为朴素的示例类似代码示例
dot的值同样转化为Variable类的实例。(如果仅仅重载一部分dot的值,一般而言函数的二阶导数将恒为0,对于这样的结果,其背后的数学内涵是深刻的。)
代码示例2.4 高阶导数实现的难点
class Variable(object):
def __init__(self, value, dot=0.):
self.value = value
self.dot = Variable(dot)
# 加法的重载
def __add__(self, other):
res = Variable(self.value + other.value)
res.dot = Variable(self.dot + other.dot)
return res
def __radd__(self, other):
return self.__add__(other)
def __str__(self):
if isinstance(self.value, Variable):
return str(self.value)
return "Variable({})".format(self.value)当然,对于一元函数,grad函数可以有相对简单的实现形式,如下所示:
def grad(fun):
def grad_f(x:Variable):
x.dot = Variable(1.)
return fun(x).dot
return grad_f 尽管这样的数据结构对于高阶导数的实现显然是必须的,但就__add__函数中类似self.d ot + other.dot这样的语句来说,当其中的self.dot 或者other.dot同样为Variable类的实例时,这里的加法将不再是浮点数之间的加法,而会转而调用Variable类中重写的__add__函数——这样就出现了运算符的循环重载问题,程序最终将会因为超过最大递归深度而报错。
>> RecursionError: maximum recursion depth exceeded.对于这一问题,一种可能的解决方案是通过巧妙的程序设计,使得我们能够根据grad函数被调用的次数来控制重载算符的递归次数,从而使得程序允许递归构建高阶导数相应的计算图。出于篇幅原因,这里不再继续展示相关程序实现的细节。
与前向模式一样,本节首先对自动微分的反向模式进行简单介绍,令读者把握反向模式的主要思想。直观上来看,反向模式的算法与前向模式相比显得极为不同,然而在
grad函数,同样能够进行一阶导数的计算。
 注
注
跳过

考虑一个特殊的计算图结构如图2.2所示,如果我们需要求出
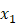

让我们来细致地考察式



由于




和










图2.2 反向模式计算图示例;函数




同时,读者可以发现,在式






由于这里对于节点的处理将会沿着计算图构建顺序的相反方向执行,这样的求导实现方式称为自动微分的反向模式,由此引出的算法又称为反向传播(back propagation)算法。
反向模式的要点在于,当我们对节点



可以验证,式




我们将用于存储节点













例如,我们可以看到,在首先对节点













同样,对节点

在对所有由








作为初始化条件,我们需要令





vjp函数,它代表着矢量-雅可比乘法(Vector-Jacobian Product)。
相较于前向模式来说,反向模式的程序实现思路似乎显得更加复杂。但从理论上来看,它和前向模式具有相当的一致性。在介绍前向模式的理论时曾讲到,如果将计算图所定义的函数


这是对式

式








下面,我们希望询问上述问题的反问题:在函数的输出

还记得前向模式之中式




这里的
我们同样可以将它写成矩阵的形式:
更加紧凑的,通过对上面的两侧求转置操作,我们可以等价地将式
不过,如果这里的





式
更加紧凑的,式
在这里,所有的


式


从计算图的视角来审视以上的求导运算,











在前向模式中,我们曾使用二元数来承接微分运算符的作用规则。而在反向模式中,我们依然希望能和前向模式一样,找到一个合理的结构来承接求导运算符的作用规则。式
注意到,对于任意的可微函数


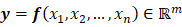

式




则我们定义函数


下面我们来考察对偶函数所具有的性质。如果函数





即在
紧接着,我们可以考虑




式
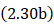
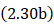








将式

在前向模式的二元数诠释中我们看到,通过将函数









其中函数

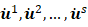





在这里,函数作用的顺序变成了

任意(可被计算机计算)的函数






式

在
举一个简单的例子,对于函数
对于输入

➢
➢
➢
第二个分量的构建是完全类似的,不过在这里我们需要首先计算乘法,再计算加法:
➢
➢
最后,采用投影算符



[5] 对于正整数




➢
也就是说,函数
这样的构建方式可以推广到可以被计算机计算的任意函数中。注意一下投影前函数的输出






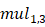





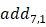


在图论中,对于具有









而在这里,如果前向模式中计算图





















作为数学形式上的比较,我们考虑函数

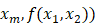

那么

这里的











这样,我们就在形式上完成了前向模式和反向模式算法的统一。
在这里,我们不加说明地给出李群对偶表示(dual representation)的定义,有相关背景的读者可以联系本节中对偶函数的定义,自行展开联想。[6]
[6] 此处暂无文献可供引用
令 









其中



与符号求导、前向模式一样,我们首先定义一个名为Variable的类作为基类,重载所需的运算操作符。其中涉及的Add、Neg、Mul、Div及Pow均为继承自Variable类的类名称。与前向模式的程序实现相比,这样模块化的程序书写方式使得代码的“颗粒感”更强,从而使得程序具有更好的可扩展性。我们在示例代码2.5.1中给出了基类Variable的程序实现。
代码示例2.5.1 自动微分反向模式的算法实现(基类Variable)
import math
from abc import abstractmethod
from typing import Tuple, Callable, List
class Variable(object):
__slots__ = ["value", "g"]
_is_leaf = True # 判断是否处于叶节点
_inherence: List = [] # 存储由该节点引出的节点
def __init__(self, value, g = 0.):
self.value = value
self.g = g
@staticmethod
def _to_variable(obj):
""" 将输入参数obj转换为Variable类 """
if isinstance(obj, Variable):
return obj
try:
return Variable(obj)
except:
raise TypeError("Object {} is of type {}, which cannot be interpreted"
"as Variables".format(obj, type(obj).__name__))
@property
def is_leaf(self):
return self._is_leaf
@property
def ready_for_backward(self,):
""" 一个节点在被反向传播之前,应该首先判断这个
节点的所有父节点是否都已经完成了反向传播,因此
需要定义这个函数来完成拓扑排序 """
for subvar in self._inherence:
if subvar.is_leaf: continue
assert hasattr(subvar, "_processed")
if not subvar._processed: return False
return True
@abstractmethod
def backward(*args):
""" 继承该类的类应该定义反向传播时的计算方法 """
pass
def __str__(self):
if isinstance(self.value, Variable):
return str(self.value)
return "Variable({})".format(self.value)
def __add__(self, other):
return Add(self, other)
def __radd__(self, other):
return Add(other, self)
def __neg__(self):
return Neg(self,)
def __sub__(self, other):
neg_other = Neg(other)
return Add(self, neg_other)
def __rsub__(self, other):
neg_self = Neg(self)
return Add(neg_self, other)
def __mul__(self, other):
return Mul(self, other)
def __rmul__(self, other):
return Mul(other, self)
def __truediv__(self, other):
return Div(self, other)
def __rtruediv__(self, other):
return Div(other, self)
def __pow__(self, other):
return Pow(self, other)
def __rpow__(self, other):
return Pow(other, self) Variable类中的_is_leaf参数用于判断节点是否处于(反向模式视角下的)叶节点, _inherence参数用于存储由现节点所引出的节点。例如,如果v3 = v1 + v2,则我们不但需要在v3节点的_args元组中分别存储v1和v2节点的地址,还需要分别在v1和v2节点的_inherence列表中加入v3节点的地址——这样的存储开销在前向模式中是不存在的。
函数ready_for_backward用于判断该节点是否能够进行反向传播。当且仅当所有由该节点所构造的节点都完成了反向传播时,即_inherence列表中所有节点的_processed参数为True时,该节点可以进行反向传播。另外,我们将Variable类的backward函数用abstractmethod这一装饰器(decorator)修饰,使得所有继承自Variable类的类,只有在定义backward函数后才可用于实例的构造。
下面我们介绍继承自Variable类的Add类,它的具体实现如代码示例2.5.2所示。
代码示例2.5.2 自动微分反向模式的算法实现(加法类Add)
class Add(Variable):
""" 计算加法 """
__slots__ = ["g", "_res", "_args", "_processed", "_is_leaf", "_inherence"]
def __init__(self, v1, v2):
"""
由两个已知的Variable节点v1和v2构造出一个新的Variable节点
参数
----
v1: Variable
位于加法操作左侧的操作数
v2: Variable
位于加法操作右侧的操作数
旁注
----
输入的参数v1和v2, 要么属于 Variable 类,要么属于继承自Variable类的子类
self.g 用于存储反向传播时该点处积累的梯度
self._res 用于存储反向传播时需要用到的参数的值
self._args 用于标记计算图中该节点的父节点
self._processed 用于标记该节点是否已经经历了反向传播的运算
"""
v1 = self._to_variable(v1)
v2 = self._to_variable(v2)
self.value = v1.value + v2.value
self._is_leaf = False
self.g = 0.
self._res: Tuple = ()
self._processed: bool = False
self._args: Tuple[Variable] = (v1, v2, )
# 更新继承关系
self._inherence: List[Variable] = []
v1._inherence.append(self)
v2._inherence.append(self)
def backward(self, ):
# 更新父节点的梯度
self._args[0].g += self.g
self._args[1].g += self.g
# 更新该节点的_processed参数
self._processed = True
return None类Add中的self.g参数对应着式

self._res中的res是英文的residue简写,用于存储函数backward中将会用到的参数。前面提到的“如果v3 = v1 + v2,则我们不但需要在v3节点的_args元组中分别存储v1和v2节点的地址,还需要分别在v1和v2节点的_inherence列表中加入v3节点的地址”,可以在Add类的初始化函数__init__中找到相应的代码实现,其中_processed参数用于标记反向传播是否完成。
与之完全类似的,我们在代码示例2.5.3~2.5.6中分别给出了取反类Neg、乘法类Mul、除法类Div及乘方类Pow的程序实现。
代码示例2.5.3 自动微分反向模式的算法实现(取反类Neg)
class Neg(Variable):
""" 计算取反操作,即 a -> -a """
__slots__ = ["g", "_res", "_args", "_processed", "_is_leaf", "_inherence"]
def __init__(self, v):
"""
参数
----
v: Variable
被取反的变量
"""
v = self._to_variable(v)
self.value = -v.value
self._is_leaf = False
self.g = 0.
self._res: Tuple = ()
self._processed: bool = False
self._args: Tuple[Variable] = (v,)
# 更新继承关系
self._inherence: List[Variable] = []
v._inherence.append(self)
def backward(self, ):
# 更新父节点的梯度
self._args[0].g -= self.g
# 更新该节点的_processed参数
self._processed = True
return None 代码示例2.5.4 自动微分反向模式的算法实现(乘法类Mul)
class Mul(Variable):
""" 计算乘法 """
__slots__ = ["g", "_res", "_args", "_processed", "_is_leaf", "_inherence"]
def __init__(self, v1, v2):
"""
由两个已知的Variable节点v1和v2, 构造出一个新的Variable节点
参数
----
v1: Variable
位于乘法操作左侧的操作数
v2: Variable
位于乘法操作右侧的操作数
"""
v1 = self._to_variable(v1)
v2 = self._to_variable(v2)
self.value = v1.value * v2.value
self._is_leaf = False
self.g = 0.
self._res: Tuple = (v1.value, v2.value)
self._processed: bool = False
self._args: Tuple[Variable] = (v1, v2, )
# 更新继承关系
self._inherence: List[Variable] = []
v1._inherence.append(self)
v2._inherence.append(self)
def backward(self, ):
# 取出更新父节点所需要的参数的值
v1_value, v2_value = self._res
# 更新父节点的梯度
self._args[0].g += v2_value * self.g # 更新v1的梯度
self._args[1].g += v1_value * self.g # 更新v2的梯度
# 更新该节点的_processed参数
self._processed = True
return None 代码示例2.5.5 自动微分反向模式的算法实现(除法类Div)
class Div(Variable):
""" 计算除法 """
__slots__ = ["g", "_res", "_args", "_processed", "_is_leaf", "_inherence"]
def __init__(self, numerator, denominator):
"""
由两个已知的Variable节点v1和v2, 构造出一个新的Variable节点
参数
----
numerator: Variable
分子(被除数),位于操作符左侧
denominator: Variable
分母(除数),位于操作符右侧
旁注
----
输入的参数numerator和denominator, 要么属于Variable
类,要么属于继承自Variable类的子类
"""
numerator = self._to_variable(numerator)
denominator = self._to_variable(denominator)
self.value = numerator.value / denominator.value
self._is_leaf = False
self.g = 0.
self._res: Tuple = (numerator.value, denominator.value)
self._processed: bool = False
self._args: Tuple[Variable] = (numerator, denominator, )
# 更新继承关系
self._inherence: List[Variable] = []
numerator._inherence.append(self)
denominator._inherence.append(self)
def backward(self, ):
# 取出更新父节点所需要的参数的值
numer_value, denom_value = self._res
# 更新分子numerator的梯度
self._args[0].g += self.g / denom_value
# 更新分母denominator的梯度
self._args[1].g += - numer_value / denom_value**2 * self.g
# 更新该节点的_processed参数
self._processed = True
return None 代码示例2.5.6 自动微分反向模式的算法实现(乘方类Pow)
class Pow(Variable):
""" 计算乘方 """
__slots__ = ["g", "_res", "_args", "_processed", "_is_leaf", "_inherence"]
def __init__(self, base, pow):
"""
由两个已知的Variable节点base和pow构造出一个
新的Variable节点,描述base ** pow
参数
----
base: Variable
乘方运算的底数
pow: Variable
乘方运算的幂
旁注
----
输入的参数base和pow, 要么属于Variable类,要么属于继承自Variable类的子类
"""
base = self._to_variable(base)
pow = self._to_variable(pow)
self.value = base.value ** pow.value
self._is_leaf = False
self.g = 0.
self._res: Tuple = (base.value, pow.value, self.value,)
self._processed: bool = False
self._args: Tuple[Variable] = (base, pow, )
# 更新继承关系
self._inherence: List[Variable] = []
pow._inherence.append(self)
base._inherence.append(self)
def backward(self, ):
# 取出更新父节点所需要的参数的值
base_value, pow_value, self_value = self._res
# 更新父节点的梯度 x^y = e^(ylnx)
# >> 更新底数梯度 y*x^(y-1)
self._args[0].g += self.g * pow_value * base_value ** (pow_value - 1)
# >> 更新指数梯度 x^y * ln(x)
self._args[1].g += self.g * self_value * math.log(base_value)
# 更新该节点的_processed参数
self._processed = True
return None 在得到了反向模式基本的数据结构之后,我们可以通过代码示例2.5.7中的函数backward_pass实现梯度的反向传播。函数backward_pass的输入var用于标记反向传播的起点节点。arg_list用于存储所有待处理的节点,它将随着程序的运行而不断更新。在程序运行的开始,列表arg_list中只有输入的var节点;当列表arg_list非空时,意味着计算图中存在尚未被处理的节点。此时,对其中的每一个元素

backward函数的递归终点,我们只需要将节点
arg_list中取出,而无须进行任何其他操作;如果通过ready_for_backward函数判断发现,节点

backward()操作,然后将构造节点
arg_list列表。计算的全过程相当于对计算图执行了反向的拓扑排序。
我们在代码示例2.5.7中给出了反向模式backward_pass函数的程序实现。
代码示例2.5.7 自动微分反向模式的算法实现(反向传播)
def backward_pass(var: Variable):
assert isinstance(var, Variable)
arg_list: List[Variable] = []
arg_list.append(var)
while len(arg_list) != 0:
# 从头开始遍历列表,找出可以进行反向传播的元素,进行反向传播
for idx, arg in enumerate(arg_list):
if arg.is_leaf:
arg_list.pop(idx)
continue
if arg.ready_for_backward:
arg_list.extend(arg._args) # 将与arg相邻的节点放入列表
arg_list.pop(idx) # 将arg从arg_list中取出
arg.backward() # 对arg参数进行反向传播 我们用不到400行代码完成了反向传播算法的程序实现。“麻雀虽小,五脏俱全”。在各种大型的自动微分库中,其反向模式的基本原理及数据结构都是与此相似的。基于反向模式,我们同样可以定义grad函数,代码示例
代码示例2.6 基于反向模式的grad函数
def value_and_grad(fun: Callable,
argnum: int = 0,)-> Callable:
'''
构造一个方程,它能够同时计算函数fun的值和它的梯度
fun: 被微分的函数,需要被微分的位置由参数argnums指定, 函数的返回只能为一个数
argnum: 可选参数,只能为整数, 用于指定微分的对象;不指定则默认对第一个参数求导
返回:
一个和fun具有相同输入结构的函数,这个函数能够同时计算fun的值和指定位置的导函数
'''
def value_and_grad_f(*args):
# 输入检查
if argnum >= len(args):
raise TypeError(f"对参数 argnums = {argnum}微分需要至少 "
f"{argnum+1}个位置的参数作为变量被传入,"
f"但只收到了{len(args)}个参数")
# 将函数的输入转化为Variable类
args_new: List[Variable] = []
for arg in args:
if not isinstance(arg, Variable):
arg_new = Variable._to_variable(arg)
else:
arg_new = arg
args_new.append(arg_new)
# 计算函数的值和导函数
value = fun(*args_new)
value.g = 1.
backward_pass(value)
g = args_new[argnum].g
# 程序输出
return value, g
# 将函数value_and_grad_f返回
return value_and_grad_f
def grad(fun: Callable,
argnum: int = 0,)-> Callable:
'''
构造一个方程,它仅计算函数fun的梯度
fun: 被微分的函数,需要被微分的位置由参数argnum指定, 函数的返回只能为一个数
argnum: 可选参数,只能为整数, 用于指定微分的对象;不指定则默认对第一个参数求导
返回:
一个和fun具有相同输入结构的函数,这个函数能够计算函数fun的梯度
'''
value_and_grad_f = value_and_grad(fun=fun, argnum=argnum)
def grad_f(*args):
# 仅仅返回导数
_, g = value_and_grad_f(*args)
return g
return grad_f 函数的测试案例与返回可以与前向模式完全相同,这里不过多赘述。利用反向模式的数据结构,我们同样可以实现函数的高阶导数计算。在前向模式中,高阶导数的难点在于限制算符重载递归的深度;而在反向模式中,高阶导数实现的难点则在于不同计算图的区分。如果在实现高阶导数的过程中同时进行高阶导数计算图的构建,将会导致同一个节点的_inherence列表同时存储不同计算图的信息,从而导致在backward_pass函数中调用ready_for_backward函数时发生错乱,带来拓扑排序的失败。
与前向模式一样,我们仅仅在这里指出在实现反向模式高阶导数时可能遇到的困难,而不再进行更深一步的讨论。
读者服务:
微信扫码关注【异步社区】微信公众号,回复“e60935”获取本书配套资源以及异步社区15天VIP会员卡,近千本电子书免费畅读。