书名：COMSOL工程传热与相变实战
ISBN：978-7-115-67261-2
本书由人民邮电出版社发行数字版。版权所有，侵权必究。
您购买的人民邮电出版社电子书仅供您个人使用，未经授权，不得以任何方式复制和传播本书内容。
我们愿意相信读者具有这样的良知和觉悟，与我们共同保护知识产权。
如果购买者有侵权行为，我们可能对该用户实施包括但不限于关闭该帐号等维权措施，并可能追究法律责任。
著 江 帆 温锦锋
责任编辑 吴晋瑜
人民邮电出版社出版发行 北京市丰台区成寿寺路11号
邮编 100164 电子邮件 315@ptpress.com.cn
网址 http://www.ptpress.com.cn
读者服务热线：(010)81055410
反盗版热线：(010)81055315
传热问题在不同的行业产生影响，需要进行详尽分析，COMSOL传热分析能够处理各种工程传热问题，是科研人员与工程师的得力工具。本书在介绍传热基本控制方程、传热分析的有限元方法、流体传热及耦合传热等理论的基础上，给出了有关基础传热、热流耦合传热、相变传热、多物理耦合传热、传热参数与结构优化、深度神经网络代理模型训练等案例分析，尽可能多地涉及COMSOL传热分析的各个方面，每个案例给出相关的背景与详细的分析过程及注意事项，为读者具体应用提供参考。
本书可作为机械、材料、水利、土木、暖通、动力、能源、化工、航空、冶金、环境、交通、电力电子、超算、医药、生物等领域的科研与工程技术人员使用COMSOL软件进行传热分析及传热参数优化的参考书，也可作为这些专业领域的本科生和研究生学习数值传热分析、有限元法及COMSOL软件的教学用书。
目前，热能科学与工程技术领域广泛采用数值传热分析软件进行模拟仿真、分析预测和设计优化，以便提高热交换效率、冷却效率、热防护效率或者降低辐射率等。因此，掌握传热机理模型及其数值计算技术对于从事各类装备设计、热管理等工作的工程师是非常必要的。而且，传热分析也是复杂装备多学科设计优化（Multidisciplinary Design Optimization，MDO）技术、热管理领域的重要组成学科。传热分析技术是复杂装备创新设计（各类设备热管理）和跨越发展的支撑技术。
数值传热分析主要是对传热控制方程求解，有很多方法，如有限差分法、有限体积法、有限单元法、边界元法等。其中有限单元法（简称有限元法，FEM）是计算椭圆型和抛物线型偏微分方程的有效数值计算方法，广泛应用于传热和固体力学计算领域。有限元分析软件可以帮助工程师解决复杂装备设计、优化或控制等环节中的传热问题。有限元分析软件很多，其中COMSOL Multiphysics具有高效的计算性能和独特的多物理场全耦合分析能力，可以保证数值仿真的高度精确，帮助科研人员与工程师分析各类传热问题，在机械工程、石油工程、能源化工、土木工程、航天航空、海洋工程、环境工程、光学工程、生物医药、电力电子、交通运输等行业的传热数值分析方面发挥着重要作用。
为了让读者掌握传热（含相变传热）分析基础知识、有限元法基础知识及COMSOL在工程传热与相变方面的应用方法，我们编写了这本《COMSOL工程传热与相变实战》。本书包含数值传热分析基础、相变基础与有限元法等基础知识及COMSOL在固体传热、流动传热、相变传热、耦合传热、参数与拓扑优化、代理模型等方面的案例分析。案例涵盖基础传热、热固耦合、热流耦合、电热耦合、相变传热等方面的工程实例，尽可能多地涉及了COMSOL的传热分析领域，案例操作步骤详细，并给出了演示视频，便于读者进一步研究。
全书共分6章，第1章介绍固体传热、流动传热、耦合传热与有限元法的基本知识，第2章介绍COMSOL的界面组成与基本操作、简单传热分析案例，第3章为传热基础分析（包括不同材质平板导热量分析、蒸汽管道的总散热量分析、建筑结构热桥分析、齿轮的渗碳与淬火分析、翅片的拓扑优化分析），第4章为耦合传热分析（包括热水壶加热过程分析、纳米流体在微通道内的流动传热特性分析、机房内的传热分析、柔性涡发生器的振荡强化传热分析、CPU散热器传热分析、双金属片的热变形分析、铜丝的通电发热分析），第5章为相变传热分析（包括孔隙尺度相变填充床储热性能分析、管道中的结冰分析、激光烧蚀分析、电池复合散热分析、微通道中蒸汽气泡生长分析），第6章为复杂传热分析（包括多孔介质传热分析、加热电路的电热固耦合分析、管式反应器温度条件优化分析、传热代理模型训练）。本书通过基础知识的介绍，让读者清楚软件中一些物理量及设置的具体意义；利用案例驱动软件学习，结合工程案例解析COMSOL在传热与相变领域应用分析的详细操作过程及一些注意事项，让读者在真实的工程分析实践中明确如何建模、设置参数及分析计算结果。本书的20多个案例涉及COMSOL传热的各个方面，让读者尽可能全面地了解传热分析的应用领域。
本书由江帆、温锦锋编写，江帆负责构思全书框架与案例筛选，并编写第1章、第2章和第6章，温锦锋编写第3章至第5章，全书由江帆统稿。
本书部分材料取自COMSOL博客、百度、知乎、哔哩哔哩等网络资源，并稍作修改，感谢这些网友所做的工作。本书编写得到广州大学各级领导，以及机械与电气工程学院老师们的支持，得到人民邮电出版社的大力支持，还得到作者家人所给予的理解与大力支持，在此一并致以深深的谢意！
本书既是从事固体传热、流动传热、相变传热、耦合传热、复杂传热及传热参数与传热结构优化等研究的工程技术人员应用COMSOL进行相关传热分析的参考书，又可作为高等院校相关专业本科生和研究生进行工程传热与数值传热分析教学、复杂传热问题（特别是多物理场耦合传热、深度神经网络求解传热等问题）研究的指导书或教学用书，本书案例的模型文件、mph文件与相关操作视频已上传至异步社区，扫描书中二维码即可领取相关资料。
因笔者的水平有限，书中难免有不当之处，敬请广大读者批评指正，请致信jiangfan2008@126.com或2908551877@qq.com，不胜感激。
江帆
2025年2月于广州
日常生活与工业生产中有很多热量传动现象与过程，直接影响人类生活方式、科技发展、工业生产和国防建设等。科学家们研究热量产生、传递和转换过程及其规律，并创建了热力学和传热学等学科。现在热力学和传热学已经在工业、农业、医学、生物、气象、信息技术等领域发挥着重要作用。在计算机技术广泛应用之前，科学家们已经对热力学和传热学的机理模型进行了深入的研究，但是只能采用傅里叶变换和参数分离等数学方法分析简单的热力学过程，在很大程度上依赖物理实验观察热量变化和传递现象、总结和验证传热规律。
近60年来，计算机技术的发展使得科学家们可以采用数值计算技术分析热量的产生、传递和转换过程，以及分析热固耦合、热流耦合、相变等复杂传热过程。计算机数值计算技术和经典传热理论的结合产生了一门新的交叉学科——数值传热学（numerical heat transfer，NHT），也称计算传热学（computational heat transfer，CHT）。数值传热学利用偏微分方程的数值计算技术（有限差分法、有限体积法、有限元法等，本书介绍有限元法）计算传热过程的状态变化（如温度场和温度梯度场的动态分布），并进一步分析预测传热过程对结构系统的影响（如固体热应力等）。数值传热分析技术及相应的计算机软件的发展，使得工程师可以十分方便地在各类工程技术领域中应用传热分析技术。
数值传热分析需要有传热分析、流体力学、有限元法等基础知识的支撑，本章简单介绍数值传热分析及相关方面的基础知识。
在科学技术领域，科学家们普遍采用系统论的方法将研究对象从环境中分离出来形成“系统”。系统观念强调了研究对象与外部环境之间的分割及联系，并且强调了系统内部要素之间的交互作用。系统与外部环境的分割或者连接之处称为系统边界。通过定义一个系统，研究者可以明确界定研究对象的边界和内涵。在与“热”相关的科学技术领域，科学家们将研究对象从环境中分割开来，并且定义为热力学系统。热力学系统是一种由“连续介质（continuum）”构成的系统，即大量的流体或者固体“质点”或者“粒子”占据连续空间位置构成一个没有缝隙的几何“体积”。采用若干参数描述热力学系统的“状态”，这些参数称为热力学系统的状态参数或者性质。热力学系统的性质不是微观尺度上单个粒子的状态，而是宏观尺度上全部粒子的统计平均规律。
一组确定的状态参数值称为热力学系统的一个状态，一个热力学系统可以具备多种状态。如果热力学系统的状态参数不随时间变化，则称热力学系统处于稳态或者平衡状态，否则称热力学系统处于瞬态或者非平衡状态。热力学系统中常见的状态参数有温度、压力、密度、内能、焓等。温度是描述热力学系统处于（瞬间）平衡状态的一个状态参数，热量是改变热力学系统状态的一种能量。
在工程技术领域，存在两门相互关联的研究热现象的学科——热力学和传热学，这两门学科分别从不同的角度研究了热力学系统的状态变化、热量传递和能量转换规律。
热力学主要研究热力学系统从一个状态变化到另一个状态时所伴随的热量变化或者热量与其他能量的转换。热力学系统与外界进行能量交换（传热或做功）的根本原因是两者的热力学状态之间存在差异。例如，热力发动机中能量发生转换是由于热力发动机的高温高压工质与外界环境的温度和压力有很大的差别。热力学第一定律和第二定律是描述热力学系统状态变化的基本定律，是热力学理论体系的基础。热力学第一定律表述为“当热能与其他形式的能量进行转化时，能的总量保持恒定”。热力学第一定律是能量守恒定律在热现象上的体现，其数学表达式为
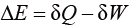（1.1）
其中，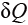
表示热量；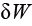
表示系统做功；ΔE是系统内能的变化量。在国际单位制中，三者的单位都是焦耳（J）。
在热力学第一定律中，进入热力学系统的热量为正，流出系统的热量为负；热力学系统对外界做功为正，外界对热力学系统做功为负；热力学系统内能增加为正，降低为负。热力学第一定律表示对于任何热力过程，系统中存储能量的增加等于进入系统的能量减去离开系统的能量。
如果热力学系统与外部环境既没有物质交换，也没有热量交换，则称为绝热系统。绝热系统中热力学第一定律的表达式为
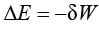（1.2）
一般传热过程中，热力学系统与环境没有物质交换，只有热量交换。如果热力学系统与外部环境既有物质交换，也有能量交换，则称为传质传热系统。
热力学第一定律表明了热力学系统中内能、热量和功这3个物理量之间的关系，但是没有说明热量传递的方向。德国物理学家克劳修斯（Clausius）指出热量不能自发地从低温物体流向高温物体，只能自发地从高温物体流向低温物体，该结论指明了自然过程中热量传递的方向，被称为热力学第二定律。热力学第二定律具有多种表述方式。热力学将传热过程分为可逆（reversible）过程和不可逆（irreversible）过程。如果一个热力学系统从初始状态经过某一路径到达一个终止状态，并且能够沿着相同路径从终止状态返回初始状态，则该传热过程称为可逆的。如果一个热力学系统从初始状态经过某一路径到达一个终止状态，但不能沿着相同路径从终止状态返回初始状态，则该传热过程称为不可逆的。Clausius引入了熵的概念描述热力学系统的初始状态和终止状态之间的差异。热力学第二定律可以表述为热力学过程中熵的变化，即
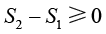（1.3）
其中，
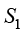和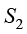
分别表示热力学系统在初始状态和终止状态的熵。一个热力学过程中，如果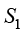和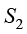相等，则该过程是可逆的；如果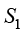小于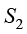，则该过程是不可逆的。
式（1.3）说明在可逆过程中孤立热力学系统的总熵保持不变；在不可逆过程中孤立热力学系统的总熵是增加的，这个规律叫作熵增加原理。因此，热力学第二定律指出在自然界中任何的热力学过程都不可能自动地复原，要使系统从终态回到初态必须借助外界的作用。
热力学第二定律明确了传热过程的可能方向和达到平衡的必要条件，以及不可逆性对过程性能的影响。所谓方向性和不可逆性，是指在各种过程中热力学系统总是从不平衡状态朝着平衡状态的方向进行。当热力学系统达到平衡状态后，一切变化也就停止了。自然过程是不可逆的，已经达到平衡状态的热力学系统不会重新自发地变为不平衡状态。例如，两个温度相等已经取得了热平衡的物体，不会自发地使得一个物体温度升高而另一个物体温度降低。因此，从本质上说，热力学系统趋于平衡就是自然过程的方向。
当热力学系统与外部环境或者系统内部存在温差时，热力学系统处于热不平衡状态，一定会造成热量传递。虽然热力学可以计算出热力学系统的两个热平衡状态之间的能量（热量）差异，但是不能计算分析两个平衡状态之间的变化过程。例如，热力学不能计算热力学系统从一个热力学状态达到另一个热力学状态所需的时间，也不能计算出某一个时刻热力学系统的非平衡状态。
传热学是研究热量传递（过程）规律的学科，可以计算热力学系统状态变化的历程。热量传递有导热、对流和热辐射这3种基本方式。物体各部分之间不发生相对位移时，依靠分子、原子及自由电子等微观粒子的振动和碰撞而产生的热量传递现象称为导热或热传导。例如，物体内部存在温差时，热量从高温部分传递到低温部分；两个直接接触的物体（固体）间存在温差时，热量从高温物体传递到低温物体，都是典型的导热现象。对于平壁一维稳态导热，它的导热热流量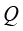
用式（1.4）计算，式中A为导热物体的表面积（m2），k为导热系数[W/（m·K）]，δ为导热物体的厚度（m），
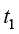和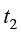
为导热物体两侧的温度（K）。平壁导热的导热密度
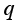用式（1.5）计算。
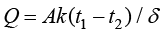（1.4）
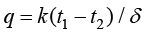（1.5）
通过流体运动把热量由某处传递到另外一处的现象，称为对流传热。对流传热分为自然对流传热（natural convection）和强制对流传热（forced convection）两类。在对流传热过程中，如果流体运动是由自身热力学状态的不平衡引起的，则称为自然对流传热；如果流体运动是由外力引起的，则称为强制对流传热。工程上常遇到的不是单纯对流传热方式，而是流体流过另一固体表面时对流传热和导热相互结合的热量传递过程，称为对流换热。对流换热的基本计算可以用式（1.6）和式（1.7），其中，h为对流换热系数[W/（m2
K）]，
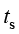和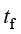
分别为固体壁面温度和流体温度（K）。
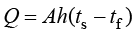（1.6）
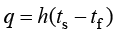（1.7）
物体通过电磁波传递能量的方式称为辐射。物体会因多种原因发出辐射能，其中因热的原因发出热辐射能的现象称为热辐射。自然界中各物体都不停地向空间发出热辐射能，热量辐射和吸收是物体间进行热量传递的主要方式之一，即辐射换热。当物体与周围的环境达到热平衡时，辐射换热量等于零；但这是动态平衡，辐射与吸收过程仍不停地进行，辐射热量与吸收热量在数量上相等。根据斯特藩−玻尔兹曼定律，物体辐射热量（或辐射力）的计算公式为
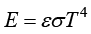（1.8）
其中，E为物体的辐射力[W/m2]；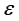
为物体的辐射率（或黑度，小于1的数）；σ为斯特藩−玻尔兹曼常数（或辐射常数），
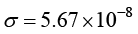W/（m2·K4）；T为黑体的热力学温度（K）。
导热和对流传热这两种热量传递方式必须通过介质才能实现，而热辐射可以在没有中间介质的真空中传递热量，这是热辐射区别于导热和对流传热的重要特点之一。当两个物体被真空隔开时，如太阳与月球之间，就不会发生导热和对流传热现象；但是太阳可以热辐射的方式将热量传给月球。热辐射过程中不仅产生能量的转移，而且还伴随着能量形式的转化。热辐射过程中，能量首先从热能转变为电磁波能，然后在吸收过程中又从电磁波能转换为热能。这是热辐射区别于导热和对流传热的另一个特点。
物理学将物质分为气体、液体和固体3种形态，传热过程可以发生在任何形态的物质中。由于许多工程设计（或分析）问题的核心是金属或者非金属固体材料中的热传递现象，因此固体材料中的传热分析占据了主导地位。这里主要探讨固体中的导热现象，即固体传热，其他传热方式可作为边界条件进行处理；后续章节中“固体”和“物体”等在概念上等同于“热力学系统”。
固体传热方式主要为热传导，研究表明如果在物体内存在温度梯度，则能量就会由高温区向低温区转移。许多学者对热传导机理进行了研究，认为当物体两端存在温度差时热量就像流体一样在物体内部流动，形成热量流（简称热流）。如同水流和电流，在单位时间内通过物体某一截面（或者表面）的热量称为热流量；单位时间内通过单位截面积（或者表面积）的流量称为热流量密度（强度），简称热流密度。物理实验表明，单位时间内通过物体单位截面积（或者表面积）的热流量（热流密度）大小正比于该截面（或表面）的法向温度梯度值，但是热流方向与法向温度梯度方向相反，即
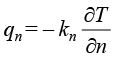（1.9）
式（1.9）也称为傅里叶方程，其中，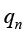
是物体截面（或者表面）法线方向的热流量密度（或热流密度），其单位为瓦/平方米（W/m2）；
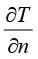是物体表面法线方向的温度梯度，其单位为开尔文/米（K/m）；常数
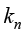称为材料法线方向的导热系数或热传导率（简称热导率，也称导热率，是表示材料热传导能力大小的物理量），其单位为瓦/（米·开尔文）[W/（m·K）]。
傅里叶方程中的负号表示热传导过程服从热力学第二定律，热量从高温区域流向低温区域。通常在笛卡儿直角坐标系中研究热力学系统的状态变化，由傅里叶方程（1.9）可得到x、y、z这3个坐标轴方向的热流密度：
;
;
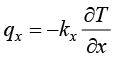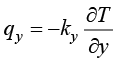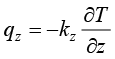（1.10）
式（1.10）中，(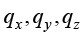
)表示x、y、z这3个坐标轴方向的热流密度；(
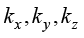)表示物体在x、y、z这3个坐标轴方向的导热系数。
导热系数是固体材料的固有性质（物性）。严格意义上，材料导热系数是与温度相关的，工程实践中为了简化计算，学者们在温度变化不大的条件下，忽略温度对导热系数的影响。理论上，固体材料中每一点在3个坐标轴方向的导热系数是不同的，即材料是各向异性的。如果物体中同一点在3个坐标轴方向的导热系数是相同的，则材料是各向同性的。如果材料中每点的导热系数不相同，即导热系数是每点位置坐标的函数，则该物体称为异构（heterogeneous）材料。如果材料中每点的导热系数相同，则该物体称为同构（homogeneous）材料。对于同构材料，物体中各点的导热系数都相同，但是每点可能存在3个不同方向的导热系数。对于各向异性的异构材料，导热系数不仅在各点不同，而且在每点3个坐标轴方向上也不同，即
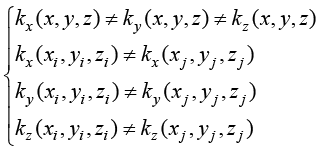（1.11）
但是，工程技术领域中的大多数材料（特别是金属材料）是各向同性的同构材料，即导热系数在每一点的3个坐标轴方向上是相等的，而且不随位置发生变化，即
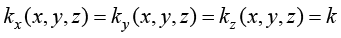（1.12）
其中，k为常数，称为材料的导热系数或者热导率。
将式（1.12）代入式（1.10），各向同性同构材料的热传导方程可表示为
;
;
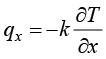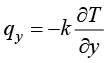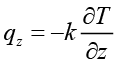（1.13）
在连续介质物理系统研究中，通常采用系统状态变量建立偏微分方程（partial differential equation，PDE）来描述质量守恒、动量守恒和能量守恒定律，因为物理系统必须遵守这些守恒规律，所以采用PDE“管理”和“控制”这些物理系统的行为。因此，这些PDE模型被称为相关物理系统的控制方程（governing equation）。在传热学中，热传导控制方程是根据热力学第一定律推导得到的能量守恒方程。通过分析（利用图1-1的直角坐标系下导热微元体推导出来，具体见文献[1]），在三维笛卡儿直角坐标系中瞬态温度场变量T(x，y，z，t)应满足的控制方程（直角坐标系下固体的导热控制方程）如式（1.14）所示。
图1-1 导热微元体
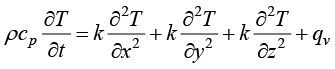（1.14）
其中，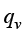
为单位时间内材料内部单位体积中产生的热量，称为内热源密度，其单位为瓦/立方米（W/m3）；
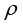为材料密度，其单位为千克/立方米（kg/m3）；cp为材料的比定压热容，即单位体积材料在确定压力下产生单位温度变化所需热量，其单位为焦耳/（开尔文·立方米）[J/（K·m3）]；
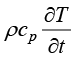表示内能的变化量。
内热源表明材料内部由某种物理或化学过程产生的热量，如电子元件中由电阻效应产生的热量。内热源qv可以是几何位置的函数，也可以是一个常量，在本书中，未加特别注明之处都将内热源作为常量。
很多工程问题需要在极坐标系和球坐标系下研究或者分析传热过程，采用基本的坐标系变换方法就可以将直角坐标系下的导热控制方程变换为极坐标系或者球坐标系下的导热控制方程。
极坐标系下导热控制方程为
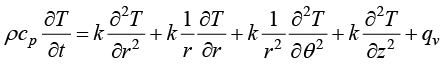（1.15）
球坐标系下导热控制方程为
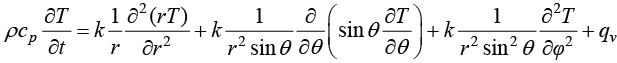（1.16）
如果温度场不随时间发生变化，则称为稳态传热过程。此时温度对时间的偏导数为零，因此式（1.14）～式（1.16）中左边为零。例如，直角坐标系下稳态导热控制方程变化为
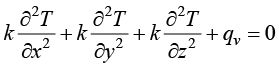（1.17）
在工程技术领域，三维空间中物体的导热模型在一定的条件下往往被简化为二维甚至一维空间的导热模型。如果物体在某一个坐标轴（为了简便假设为z轴）方向没有热量传递，即温度场对z轴的偏导数为零，则此时物体中的导热过程就可以简化为二维空间的导热过程。
在直角坐标系下，由三维空间的导热控制方程得到二维平面导热控制方程，即
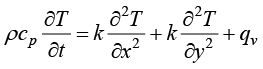（1.18）
假设物体内部不产生热量，即没有内热源项，则二维平面导热控制方程（1.18）等同于
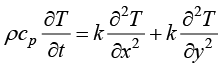（1.19）
假设物体内部不产生热量并且温度不随时间变化（稳态温度场），则二维平面导热控制方程（1.18）等同于
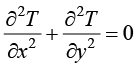（1.20）
如果进一步假设物体在两个坐标轴方向没有热量传递，则三维物体的传热过程就可以被简化为一维传热过程。在直角坐标系下，由二维空间的导热控制方程（1.18）可以得到一维空间导热控制方程
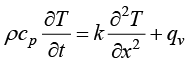（1.21）
由式（1.21）知，一维稳态导热控制方程可退化为一个二阶常微分方程
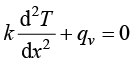（1.22）
一维稳态导热过程具有理论通解
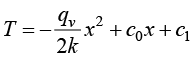（1.23）
为了求得式（1.23）的确定解，需要补充其他条件才能计算其中的两个系数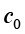
和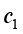
。
在数学形式上，导热控制方程式（1.14）～式（1.19）是二阶偏微分方程（second-order partial differential equation）。在工程技术领域，二阶偏微分方程占据了主导地位，许多物理系统的控制方程都是二阶偏微分方程，故这里简单介绍二阶偏微分方程的基本性质。
假设函数u是n维实数空间的一个标量函数，则关于函数u的二阶偏微分方程通式为
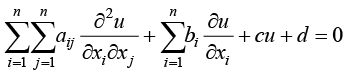（1.24）
如果采用爱因斯坦求和约定，式（1.24）可以简写为
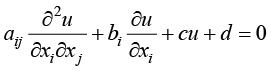（1.25）
在式（1.24）或者式（1.25）中，如果d=0，则称方程为齐次（homogenous）方程；否则称为非齐次（non-homogenous）方程。在偏微分方程中，如果函数u及其偏导数项的系数中不包括函数u（或偏导数），则称为线性偏微分方程；在偏微分方程中，如果函数u及其偏导数项的系数中包括函数u（或偏导数），则称为非线性偏微分方程。
如果实数空间的维数等于2（只有两个自变量），则函数u的二阶偏微分方程通式简化为
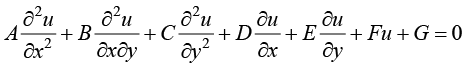（1.26）
1.2.2节介绍的导热控制方程都是线性偏微分方程。导热控制方程中，如果考虑导热系数随温度的变化，则导热控制方程变化为非线性偏微分方程。例如，在导热系数随温度变化但变化率较小的情况下，二维导热控制方程就变为非线性形式，即
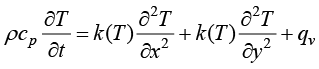（1.27）
对于二阶线性偏微分方程，通常分为椭圆型、抛物线型和双曲线型3种类型。偏微分方程（1.26）的类型是由式中二阶偏导数项的系数所决定的。如果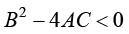
，则偏微分方程（1.26）是椭圆型（elliptic）。椭圆型偏微分方程描述与时间无关的物理过程，如稳态传热过程。椭圆型偏微分方程中不包含时间变量，仅包含空间变量。从另一个角度，椭圆型偏微分方程描述与时间相关的物理过程当时间趋于无穷大时的极限状态。
如果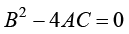
，则式（1.26）所示的偏微分方程是抛物线型（parabolic）偏微分方程。抛物线型偏微分方程描述与时间相关的“传播（propagation）”过程，如瞬态传热过程。抛物线型偏微分方程中不仅包含空间变量，还包含时间变量（通常为一阶时间偏导数）。在空间域上，抛物线型偏微分方程一般是椭圆型偏微分方程。因此，抛物线型偏微分方程描述一个由无数的“中间平衡状态（椭圆型）”构成的物理过程，并且当时间趋于无穷大时，抛物线型偏微分方程的解无限趋近于相应的椭圆型偏微分方程的解。
如果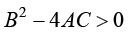
，则式（1.26）所示的偏微分方程是双曲线型（hyperbolic）偏微分方程。双曲线型偏微分方程也描述与时间相关的“传播（propagation）”过程，如波动过程。双曲线型偏微分方程中不仅包含空间变量，而且包含时间变量（一般为二阶时间偏导数）。在空间域上，双曲线型偏微分方程一般也是椭圆型偏微分方程。双曲线型偏微分方程描述“椭圆型平衡状态”像波一样传播的物理过程。
因此，式（1.20）所示的稳态导热控制方程是椭圆型二阶偏微分方程。如果偏微分方程中自变量数目大于2，则需要分别对两个自变量组合来判断偏微分方程的类型。瞬态导热控制方程对于任意两个空间坐标都是椭圆型二阶偏微分方程，但是对于时间和任意一个空间坐标则是抛物线型二阶偏微分方程。在物理系统中，科学家们一般以时间变量为主要参考变量，因此，瞬态导热控制方程被称为抛物线型二阶偏微分方程。
二阶偏微分方程的类型是其固有的性质，不随坐标系改变发生变化。即在某个坐标系下，如果一个二阶偏微分方程是椭圆型（抛物线型或者双曲线型），则在另外的坐标系下，它仍然是椭圆型（抛物线型或者双曲线型），具体证明可参考文献[1]。
根据高等数学知识，一个数学函数的积分原函数是一组函数簇，称为积分问题的通解（general solution）。例如，没有内热源的一维稳态导热控制方程的通解为
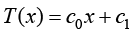（1.28）
由于式（1.28）包含了两个未知系数，因此需要给定温度函数在两个点的值，才能得到一维温度场函数的特定解（particular solution），也称为定解。假设已知温度场在两个端点的温度值为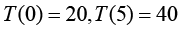
，将这两点的温度值代入式（1.28），就可以得到一维温度场的定解为
。
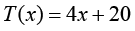这种给定物理场在边界点上值，称为物理问题定解的边界条件（boundary condition）。椭圆型偏微分方程只需给定边界条件就可以获得定解，因此被称为边值问题（boundary value problem）。对于包含时间变量的通解函数（如瞬态传热问题），还需要知道某一时刻的全部函数值，才能确定问题的定解。例如，传热分析问题中，一般给定物体在初始时刻的温度分布，这也称为初始条件（initial condition）。对于双曲线型偏微分方程，初始条件不仅包括函数的初始值，还包括函数一阶偏导数的初始值。
在偏微分方程计算领域，为了得到一个数学问题的定解，必须预先给定边界条件和初始条件。因此，以抛物线型或双曲线型偏微分方程描述的物理问题在数学上通常称为连续初始边（界）值问题（initial boundary value problem），边界条件和初始条件称为该问题的定解条件。
通常将连续初始边值问题的边界条件分为三类，分别称为Dirichlet条件、Neumann条件和Robin条件。连续初始边值问题的三类边界条件具体描述方式如下。
Dirichlet条件的数学形式为
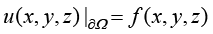（1.29）
其中，u(z，y，z)为连续初始边值问题的解；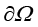
为问题定义域边界；
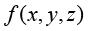为已知函数或者常数。
Neumann条件的数学形式为
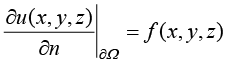（1.30）
其中，各项的含义与Dirichlet条件中各项的含义相同，Neumann条件表示解函数在定义域边界上的法向梯度为已知函数或者常量。
Robin条件的数学形式为
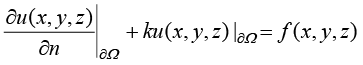（1.31）
其中，各项的含义与Dirichlet条件中各项的含义相同，Robin条件为Dirichlet条件和 Neumann条件的组合，也称为混合边界条件。
Dirichlet条件和Neumann条件是Robin条件的特例。令Robin条件中的系数k=0，则得到Neumann条件；令k→∞，则得到Dirichlet条件。
边界条件实质上描述了“系统”与外部环境在分界处的物质和能量传递；只有清楚地描述和分析环境对系统的影响才能确定系统的具体状态（定解）。初始条件相当于某一个物理过程开始时系统的初始状态，即一个物理过程的起点状态。
偏微分方程的边界条件，即Dirichlet条件、Neumann条件和Robin条件，在各科学领域的表现形式和物理含义是完全不相同的。在传热学中，有四类典型的边界条件表现形式。
第一类边界条件是指物体边界上的温度函数为已知，在三维直角坐标系中
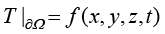（1.32）
其中，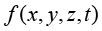
为已知的数学函数或者常数。第一类传热边界条件就是Dirichlet条件在传热学中的具体表现形式。第一类边界条件表示物体边界温度被强制维持在一条已知的随时间变化的曲线上或者固定曲线上，物体边界甚至可能保持一个恒定的温度。
第二类边界条件是指系统边界上的热流密度已知，根据式（1.9）可表示为
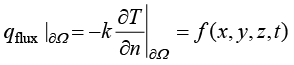（1.33）
其中，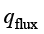
为边界上外法线方向的热流密度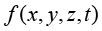；为已知的数学函数或者常数。第二类热边界条件实质是Neumann条件在传热学中的具体表现形式。第二类热边界条件表示物体边界上流出（入）的热流密度是已知的函数，或者为一常数。注意，热流密度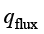与边界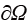
外法线方向相同，即热量从物体向外流出时取正值，相反热量流入物体时则取负值。
第三类边界条件描述物体与环境的对流换热现象，即流体流动通过物体表面实现热量交换，又称为对流换热边界条件。第三类边界条件的数学方程为
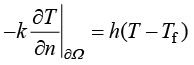（1.34）
其中，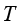
为固体温度；
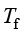为流体介质的温度；
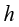为换热系数，单位为瓦/（平方米·开尔文）[W/（m2·K）]。
第三类换热边界条件表明固体边界热流密度与固体和流体之间的温度差成正比，实质上是Robin条件的一种表现形式。一般情况下，流体温度和换热系数设置为常数，特殊情况下可以是温度、时间与位置的某种函数。换热系数与流体物性、流动速度、流体和固体之间的温差等因素相关，多数情况下需要采用实验方法测定。需注意的是，式（1.34）表示热量从固体向外流出传递到流体中；当热量从流体介质流入固体时此公式仍然正确。
传导和对流都要通过介质进行传递，但是电磁波辐射机理不同，热辐射能可以在完全真空中传递。热力学的研究表明：理想的辐射体（黑体）向外发射能量的速率与它的绝对温度的4次方成正比。一个物体向另一个物体发送热辐射能的同时，也接收另一个物体的热辐射能。所以，在一个物体通过热辐射与另一个物体进行热量交换时，其边界热流密度可用式（1.35）计算，即
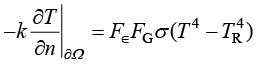（1.35）
其中，T为物体的边界温度；TR为环境温度（或其他物体的温度）；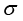
为比例常数，称为斯特藩−玻尔兹曼常数；
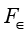为辐射率函数；
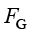为几何“视角系数”（view factor）函数，这两个函数与结构的几何形式是密切相关的。
热辐射边界条件实质上仍然是Robin条件的一种表现形式。
初始条件描述热力学系统初始时刻的状态，是瞬态传热过程分析的基础，其表达式为
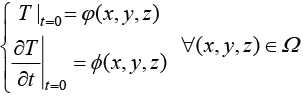（1.36）
其中，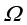
为系统定义域；
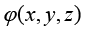与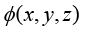
是已知函数（随位置坐标而变化）或者常量。在工程技术领域，一般的瞬态传热分析过程多假设系统的初始温度为常量（如环境温度）。
通常情况下，偏微分方程形式的物理系统控制方程（如导热控制方程）只有特殊情形才存在解析解。对于简单的偏微分方程，可采用变量分离和拉普拉斯变换等方法进行解析求解。但是，目前大多数偏微分方程仍然不能采用解析方式求解，只能采用数值计算方法在离散点上“逼近”求解。
偏微分方程离散化的方式不同，形成了许多不同的数值解法。有限差分法（finite difference method，FDM）、有限体积方法（finite volume method，FVM）或者控制体积方法（control volume method，CVM）以及有限元法（finite element method，FEM）是工程技术领域广泛应用的偏微分方程数值计算方法。
有限元法是应用最多的偏微分方程数值计算方法，广泛应用于固体力学中的结构变形分析和传热学中的温度场分析，并且逐渐应用于流场分析。有限元法可以很好地适应不规则几何区域，一般情况下可获得高精度数值解。
首先，有限元法将连续的系统全局定义域分解为一组“有限数目”离散的子定义域，这些子定义域称为单元。单元可以具有多种几何形状，因此能更好地逼近几何形状复杂的系统定义域（特别是边界区域）。
其次，有限元法在局部子定义域上（每一个单元内）构造一个近似函数，也称为实验函数（trial function），代替全局定义域上待求的物理场函数。有限元法在单元内若干节点上选择未知的物理场函数值来构造一个插值函数作为实验函数。这样，未知的物理场函数在各个节点上的数值就成为离散化物理系统的未知量（自由度），从而使一个连续的无限自由度问题变成一个离散的有限自由度问题。
最后，有限元方法通过积分形式将全部单元内的实验函数转化为代数方程组。针对具体的物理问题，有限元法可以采用变分法（variational method）、虚功原理（virtual work principle）和加权余量法（weighted residual method）等方法建立单元的代数方程。变分法建立实验函数的泛函，然后采用变分求驻值（stationarity）方法建立有限单元模型。变分法的数学推导过程清晰完备，物理意义上体现了系统内总能量最小的原则。变分法的困难在于寻找物理场函数的泛函，不是所有的物理场函数都能建立相应的泛函。
虚功原理体现了外力与内力平衡的原则，即处于平衡状态的力学系统中针对任何虚位移全部外力做功等于全部内力做功。虚功原理方法主要应用于固体力学和结构力学分析领域。
加权余量法认为每个单元内的实验函数与真实的物理场函数之间必然存在误差，在全部单元内将两个函数差进行加权积分，通过令全局积分加权余量为零建立有限元模型。加权余量法不需要寻找物理场函数的泛函，所以其适用范围更广，数理分析过程也更为简单，实用意义已经超过变分法。
本节采用加权余量法推导平面热传导问题的有限元模型。根据式（1.18）得到平面热传导控制方程的微分形式为
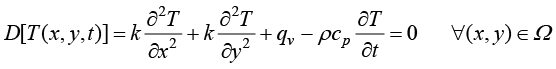（1.37）
其中，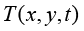
是全局定义域Ω上未知的温度场函数，因不能采用解析方式获得全局温度场函数，故采用数值计算方法构造实验函数
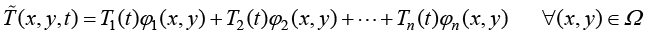（1.38）
来近似地代替真实的温度场函数。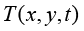
式（1.38）中，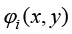
为已知的基函数；
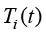为待求温度场函数在若干节点的数值。在数学形式上，实验函数就是基函数的线性组合。式（1.38）表明与时间相关的瞬态传热过程可以近似分解为两部分：只与几何域相关的基函数、只与时间域相关的节点温度。
由于实验函数不可能在全局定义域的每一点上都等于未知的温度场函数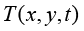，加权余量法令实验函数在定义域上的积分余量为零，即
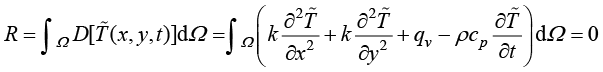（1.39）
其中，R表示热传导微分控制方程的积分余量。这样，式（1.39）就构成了一个以一组几何点的温度值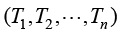
为未知量的线性代数方程。由于实验函数
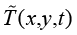包含n个未知参数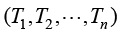，因此需要构造n个线性独立的代数方程。为此，采用加权余量法选择n个加权函数构造加权的积分余量，获得n个线性独立的加权代数方程：
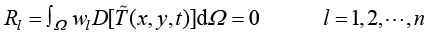（1.40）
其中，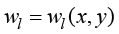
为已知的加权函数；
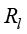表示热传导控制方程采用
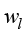权函数时的加权积分余量。
由式（1.40）可以得到
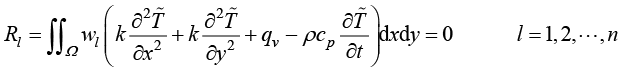（1.41）
采用分部积分方法，将式（1.41）变化为
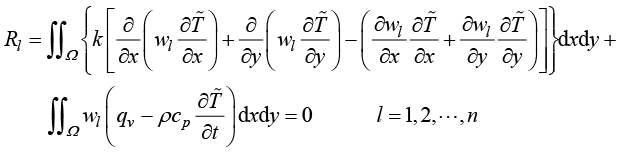（1.42）
在微积分学中，面积积分可以通过格林公式转换为线积分，即
（1.43）
根据格林公式，式（1.42）的第一项可表示为
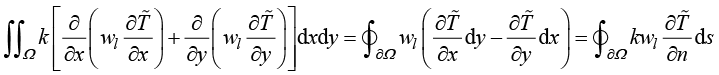
（1.44）
将式（1.44）代入式（1.42）中，平面温度场加权余量变换为
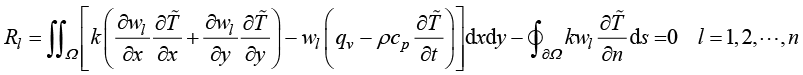
（1.45）
式（1.45）对于平面传热系统的全局定义域成立。但是，有限元法并不是在全局定义域上构造一个全局实验函数来计算全局加权余量，而是在每个单元（子定义域）上构造一个局部实验函数来计算局部加权余量，并且累加全部局部加权余量得到全局加权余量。在每个单元上，实验函数的未知参数选择为单元节点的温度值，未知参数的数量等于单元节点数量。
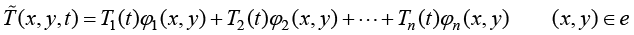（1.46）
这样，定义域离散化后，在每个单元上都可以得到一个加权积分余量
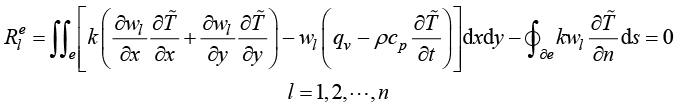
（1.47）
其中，e为单元子域；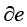
为单元边界。令式（1.42）中权函数的数量n等于单元节点数目，就可以得到n个加权余量。
在加权余量法中，权函数直接影响最终代数方程组的形式和计算精度。已经出现多种加权函数的构造方法，其中迦辽金加权函数方法得到广泛认可。迦辽金法采用实验函数对待求参数（节点温度）的导数构造加权函数，即
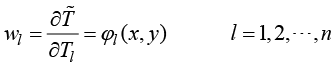（1.48）
因此，迦辽金加权余量方法构造的有限元模型的具体形式取决于单元的基函数形式。在后续内容中将介绍各种类型单元中基函数（形函数）的构造方法，并且进一步推导相应的有限元模型。注意，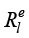
表示在单元e内关于节点l的加权积分余量，它一般情况下不等于零；有限元法假设在全部单元内关于同一节点的加权余量和为零，即
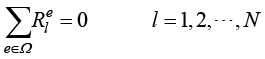（1.49）
其中，加权余量的下标l表示节点在网格中的全局编号；N为全部网格节点数量。因此，式（1.49）构成了N个代数方程，联立求解可以得到全部网格节点在某一时刻（或者时间步）的温度值。
有限元法等各类数值计算方法采用近似的实验函数代替精确的物理场函数，即有限元模型中的物理场函数永远是近似的实验函数。因此，为了书写方便，在后续内容直接将实验函数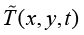
表示为。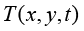
对于二维物理（传热）系统的几何定义域，有限元法通常采用三角形网格来划分。三角形单元对复杂几何轮廓有较强的适应能力，很容易通过增加三角形网格数量来精确地逼近（拟合）复杂的几何边界。因此，三角形网格在二维有限元分析中得到广泛应用。各种有限元软件都将三角形网格作为基本的单元形式，很多文献也主要以三角形单元为基础介绍有限元法。
如图1-2所示，典型的三角形网格选择3个顶点作为物理场（温度场）函数的插值节点，因此称为3节点三角形单元。3节点三角形单元一般采用i、j和k，以逆时针方向顺序标识3个顶点。
图1-2 3节点三角形单元
有限元法在三角形单元（包括其他类型单元）中一般采用多项式函数构造近似的实验函数。因为多项式实验函数是通过节点函数值插值方式得到，所以单元的实验函数通常称为物理场插值函数。在传热分析中，单元的实验函数称为温度场插值函数；在结构分析中，实验函数则称为单元的位移插值函数或者位移模式。
单元温度场插值函数的阶数由选择的插值点数目决定，在3节点三角形单元中，只能选择3个节点的温度值，因此单元温度场插值函数只能是一次多项式，即
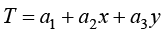（1.50）
其中，T表示单元域内任意一点(x, y)的温度；a1、a2、a3为待定系数。为了确定温度场插值函数的待定系数，将3个节点的温度值Ti、Tj、Tk及坐标代入式（1.50），可得
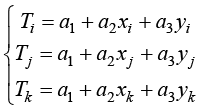（1.51）
根据上述线性方程组，可以进一步求出插值函数的系数
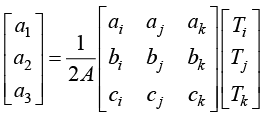（1.52）
其中，
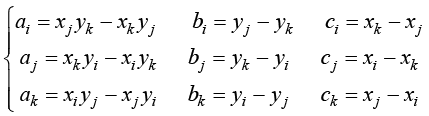（1.53）
式（1.52）中，A为三角形ijk的面积，其计算式为
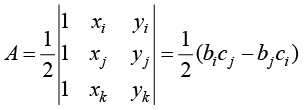（1.54）
由式（1.53）可以得到
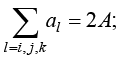
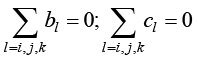（1.55）
将式（1.52）代入式（1.50），得到单元内温度插值函数，即
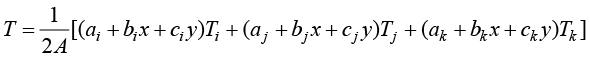（1.56）
令
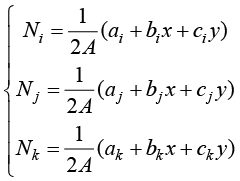（1.57）
则3节点三角形单元的温度场插值函数可以写作
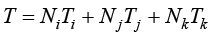（1.58）
其中，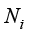
、
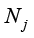和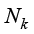
就是实验函数的基函数，称为三角形单元顶点的形状函数（简称形函数）。
从式（1.58）可以看出，三角形单元任何一点的温度值都是3个节点温度值的线性组合，单元形函数反映了3个节点温度值对单元任一点温度的影响程度，即单元形函数是一种比例系数（函数）。根据形函数的定义，可以得到形函数的以下性质：
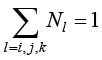（1.59）
以及
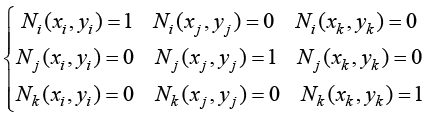（1.60）
上述三角形单元形函数性质具有明确的几何意义。如图1-3所示，连接三角形单元中任一点p(x,y)与3个顶点形成3个子三角形。随后分别标记3个子三角形Δpjk面积为Ai，Δpki面积为Aj，以及Δpij面积为Ak；并且标记三角形单元Δijk的面积为A。
图1-3 三角形面积坐标
令
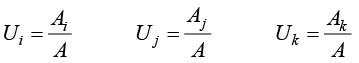（1.61）
Ui、Uj和Uk称为一个点在三角形单元内的面积坐标，可以决定一个点在三角形中的位置。因为3个子三角形的面积之和为原三角形单元的面积，所以
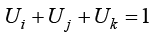（1.62）
3个子三角形的面积可以表示为
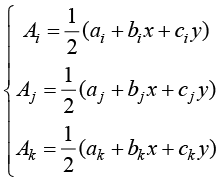（1.63）
因此，面积坐标就是三角形顶点的形函数，即
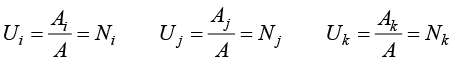（1.64）
有限元法采用面积坐标可以推导得到三角形上的函数积分的解析表达式，有利于单元刚度矩阵和载荷向量的计算。
式（1.58）所示的温度场插值函数适用于整个单元区域，其在一条单元边上退化为更简单的线性插值关系。如图1-4所示，单元边界jk上任一点的温度T应该与Ti无关，是Tj和Tk的线性组合，即
图1-4 三角形单元边上温度场插值示意
（1.65）
其中，参数变量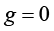
对应于节点j，
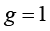对应于节点k。
三角形单元边jk的长度为
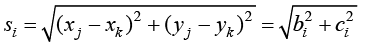（1.66）
单元边长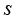变量
与参数变量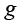
之间可建立如下关系式：
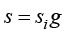（1.67）
其微分关系为
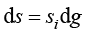（1.68）
在有限元法中，如果一个三角形单元的三条边都没有处于系统全局定义域的边界上，即三角形的3条边分别是另外3个三角形的单元边，则称此三角形为内部单元。反之，如果一个三角形单元中有一条或者两条边位于系统全局定义域边界上，则称此三角形为边界单元。
如果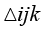
为内部单元，则对于式（1.47）所示的加权余量积分式，其边界线积分项中的法向温度梯度必然与相邻单元的法向温度梯度大小相等且方向相反，在全部单元加权余量相加时，两个相邻单元在同一条边上的线积分项相互抵消。因此，建立内部单元的加权余量模型时，有限元法不必计算式（1.47）中的线积分项。有限元法只需在边界单元的边界边上计算线积分项，而且边界单元的非边界边上也不必计算线积分项。
在内部三角形单元中，采用迦辽金权函数
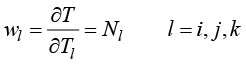（1.69）
根据积分需要，权函数对坐标求偏导数得到
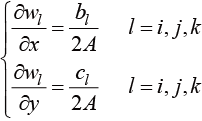（1.70）
温度插值函数对空间坐标的偏导数为
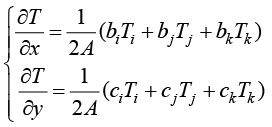（1.71）
同理，温度插值函数对时间坐标的偏导数为
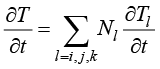（1.72）
将式（1.69）～式（1.72）代入式（1.47）得到
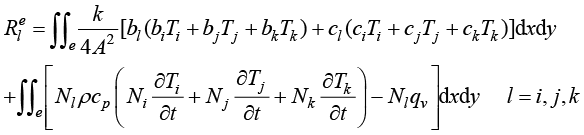（1.73）
进一步整理得到
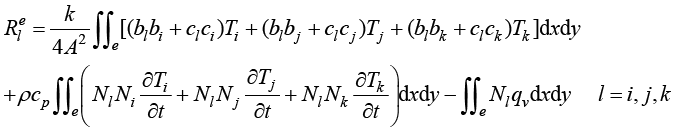（1.74）
将3个加权函数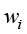
、
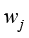及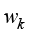
的加权积分余量合并写作矩阵形式为
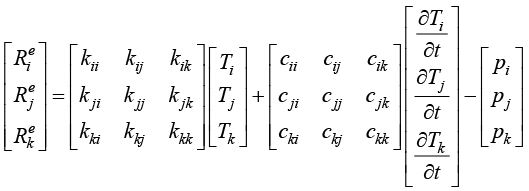（1.75）
式（1.75）也可以简写为
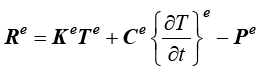（1.76）
其中，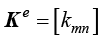
称为单元温度刚度矩阵，是一个对称矩阵，其元素计算公式为
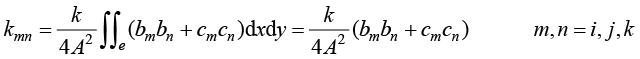（1.77）
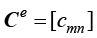称为单元的热容矩阵，也是一个对称矩阵，每个元素的计算公式为
（1.78）
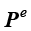为内热源产生的单元节点温度载荷列向量，其元素计算公式为
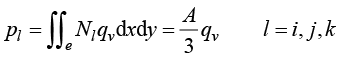（1.79）
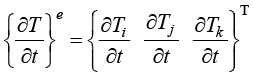是单元节点温度关于时间的导数的列向量。
有限元法采用式（1.76）～式（1.79）建立边界单元的加权余量模型，然后需附加计算边界单元的线积分项，使之满足边界条件。注意并非边界单元的3条边都是边界边，一个三角形单元至多有两条边为边界边。通常，有限元软件系统可以在网格划分时采用网格细化方法使得一个三角形单元只有一条边界边，因此，下面只讨论三角形单元的一条边为边界边的情况。
假设三角形单元的一条边jk为边界边，由式（1.65）所示的边界温度插值函数表达式，可得边界上的迦辽金权函数为
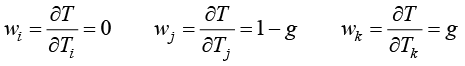（1.80）
根据式（1.32），第一类边界条件表示相应边界段上的温度为已知常数或者可以由已知函数计算得到确定值。假设一个边界单元中jk边位于第一类边界段上，则有限元法将该单元的边界节点温度设置为给定值
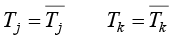（1.81）
其中，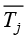
和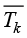
分别为已知的j与k节点温度值，通常两者相等。
第二类边界条件表示相应边界段上的热流密度为已知常数或者可以由已知函数计算得到确定值。假设一个边界单元中jk边位于第二类边界段上，将第二类边界条件（1.33）和边界边上的迦辽金权函数（1.80）代入加权余量（1.47）的线积分项中，可得三角形边界单元由热流密度产生的节点载荷
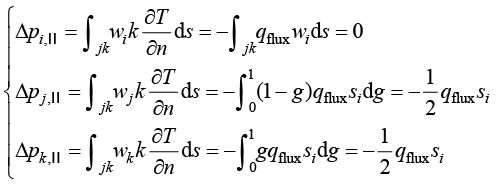（1.82）
其中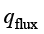，表示边界热流密度（常量）；
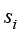表示边界边的长度。
由式（1.82）可知，线积分项对边界单元的温度刚度矩阵没有影响，边界单元只需在内部单元节点的温度载荷列向量的基础上，增加由边界热流密度产生的节点载荷。
假设一个边界单元中jk边位于第三类边界段上，将第三类边界条件（1.34）和边界边上的迦辽金权函数（1.80）代入加权余量（1.47）的线积分项中，可得
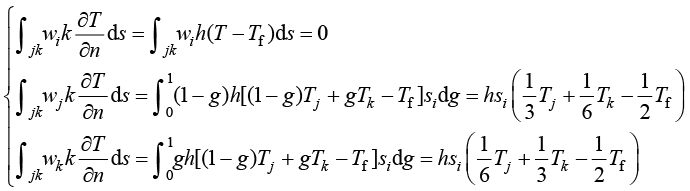
（1.83）
其中，h表示对流换热系数（常量）；Tf表示流体温度（常量）；si表示边界边的长度。
在对流换热边界条件下，线积分项中出现了节点温度项，因此对边界单元的温度刚度矩阵有影响。边界单元的温度刚度矩阵需要在内部单元的温度刚度矩阵的基础上增加以下元素的变化：
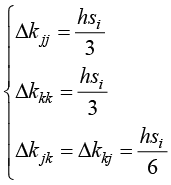（1.84）
同时边界单元需在内部单元节点的温度载荷列向量的基础上，增加由对流换热产生的节点载荷
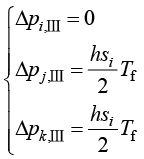（1.85）
假设一个边界单元中jk边位于热辐射边界段上，将热辐射边界条件（1.35）和边界边上的迦辽金权函数（1.80）代入加权余量（1.47）的线积分项中，可得
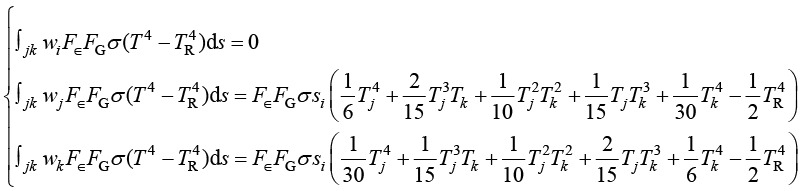
（1.86）
在热辐射边界条件下，线积分项中出现了节点温度项，因此对边界单元的温度刚度矩阵有影响。边界单元的温度刚度矩阵需要在内部单元的温度刚度矩阵基础上增加以下元素的变化：
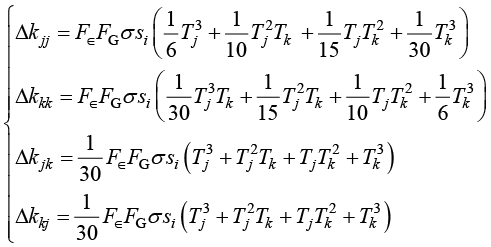（1.87）
据式（1.87）可知，热辐射边界使得有限元模型演变为非线性代数方程，因此计算比较复杂。一般来讲，非线性代数方程组求解需要采用给定初始值并迭代计算的方法。在瞬态温度场分析过程中，如果时间步足够小，则可以采用tn−1时刻的温度值计算tn时刻温度刚度矩阵。
边界单元需在内部单元节点的温度载荷列向量（1.79）的基础上，增加因热辐射产生的节点载荷
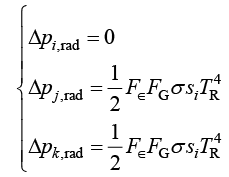（1.88）
如图1-5所示，典型的4节点四边形单元选择4个顶点为插值节点，并且以逆时针方向将节点编码为i、j、k和l；单元内部温度场采用双线性多项式（bilinear polynomial）插值函数，即
图1-5 任意形状的4节点四边形单元
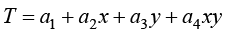（1.89）
其中，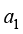
、
、
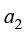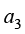和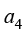
为待定系数。
式（1.89）被称为双线性多项式函数，这是因为如果其中一个变量固定，则变成另一个变量的线性函数，这样可以得到两个线性函数；另外，式（1.89）可以表示为两个线性函数的乘积形式。根据1.6节的知识，可以得到4节点四边形单元的加权余量模型如下。
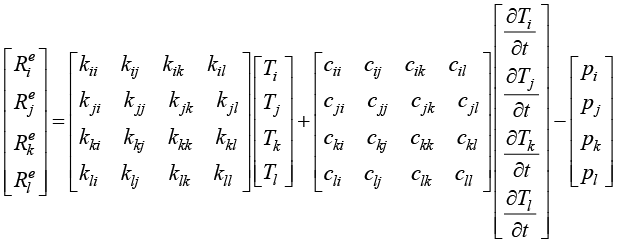（1.90）
其中，单元温度刚度矩阵元素为
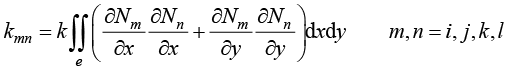（1.91）
单元热容矩阵元素为
（1.92）
由内热源产生的单元温度载荷列向量为
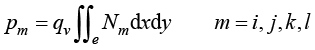（1.93）
任意4节点四边形单元中温度插值函数的系数计算十分困难，而且刚度矩阵、热容矩阵及载荷向量表达式中有些积分项无法得到解析的原函数。所以，有限元法不直接计算任意形状的四边形单元模型，而是采用等参映射方法间接计算四边形单元模型。
物理系统（传热系统）所在的几何空间称为物理空间，其坐标系称为全局坐标系；理想的正方形所在的几何空间称为参数空间，其坐标系称为局部坐标系。如图1-6所示，坐标变换方法将参数空间ξOŋ坐标系中的规则正方形单元映射到物理空间xOy坐标系下的任意四边形单元。参数空间中几何形状向物理空间中几何形状的映射函数可表示为
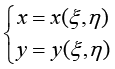（1.94）
通过映射，在物理空间中一个函数的面积积分可以转化为参数空间中的面积积分，如下式所示。
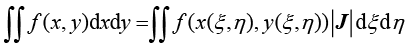（1.95）
其中，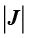
为雅可比矩阵的行列式，雅可比矩阵为
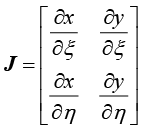（1.96）
图1-6 任意四边形单元与正方形单元之间的映射
在参数空间向物理空间映射过程中，有限元法在两类四边形单元的顶点之间建立一一映射关系。假设参数空间中正方形单元与物理空间的四边形单元的顶点标号都为i、j、k、l，则等（节点）参数映射函数为
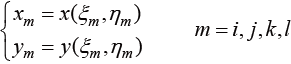（1.97）
虽然映射函数式（1.97）可以采用多种形式的插值函数，但是工程实践中一般采用多项式插值函数。因为参数空间中的正方形和物理空间中的任意四边形都只有4个节点，所以参数空间向物理空间的几何坐标映射函数采用双线性插值函数，即
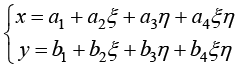（1.98）
对于物理空间中不同的四边形单元，具体的双线性函数的插值系数是不同的。将物理空间中一个四边形单元4个节点的全局坐标值代入式（1.98），就可以得到参数空间标准正方形到该四边形单元的映射函数（系数）。
注意，等参映射方法仅仅保证物理空间四边形单元顶点与参数空间正方形顶点之间的一一映射，并不能保证任意形状四边形单元与正方形单元中每个几何点映射的一致性。另外，具体的等参数映射函数与参数空间正方形的尺寸和位置有关。接下来在参数空间中选择两种正方形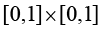
和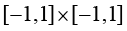
作为参考正方形单元，分别推导坐标映射函数和温度插值函数。
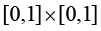的等参映射函数如图1-7所示，在参数空间中选择参考正方形为一个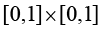正方形，即参数空间中正方形顶点的坐标分别为i(0,0)、j(1,0)、k(1,1)和l(0,1)。将物理空间中任意四边形单元顶点的全局坐标和参数空间中正方形顶点的局部坐标值代入式（1.98），就可以求出参数空间正方形到物理空间任意四边形的映射函数中的待定系数，如式（1.99）所示。
（1.99）
图1-7 参数空间与物理空间之间的四边形等参映射
将式（1.99）代入式（1.98），得到参数空间中正方形到物理空间中任意四边形的映射函数，即
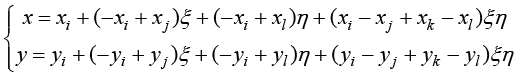（1.100）
有限元法一般将参数空间标准正方形向物理空间任意四边形的映射函数写成节点形函数的组合形式，即
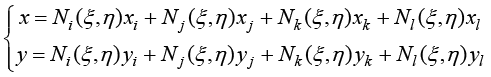（1.101）
其中，局部坐标向全局坐标映射中的节点形函数可表示为
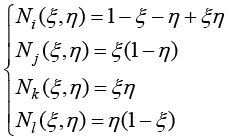（1.102）
在参数空间中，正方形单元的温度场插值函数同样采用双线性插值函数，即
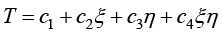（1.103）
将正方形4个节点坐标和节点温度值代入式（1.103），可得到温度场插值函数的待定系数，即
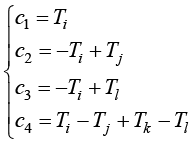（1.104）
因此，参数空间中正方形单元温度场插值函数同样可以变换为节点形函数组合形式，即
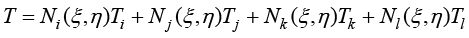（1.105）
其中，正方形单元温度场插值函数的节点形函数与几何映射函数中节点形函数完全相同。
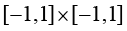的等参映射函数如图1-8所示，在参数空间中选择另一种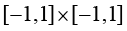正方形，即参数空间中正方形顶点的坐标分别为i(−1,−1)、j(1,−1)、k(1,1)和l(−1,1)。同理，将物理空间任意四边形单元顶点的全局坐标和参数空间正方形顶点的局部坐标值代入式（1.98），可以求出其中的待定系数。同样，可以将参数空间中
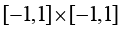正方形向物理空间中四边形的几何映射函数写成式（1.101）的形式，其中正方形节点形函数为
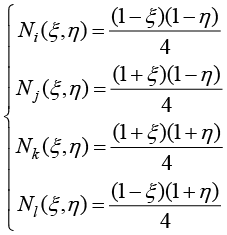（1.106）
图1-8 参数空间与物理空间之间的四边形等参映射
在参数空间中，正方形单元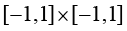的温度场插值函数同样采用式（1.103）形式的双线性插值函数。代入正方形4个节点坐标和节点温度值，可计算出温度场插值函数中的系数。同样，将温度场插值函数写成节点形函数的组合形式，温度场插值函数的节点形函数与几何映射函数中节点形函数完全相同。
可以验证上面推导的4节点正方形单元的节点形函数满足节点形函数的基本性质，即
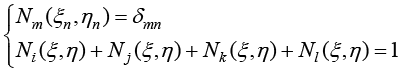（1.107）
在物理空间的四边形单元上计算平面传热模型时，首先需要计算温度场的梯度函数。然而，式（1.103）所示的温度函数定义在局部坐标系内，因此它对全局坐标系(x,y)不存在显式函数关系，采用链式求导方法可得
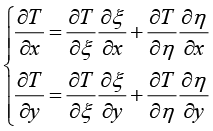（1.108）
由于没有坐标系(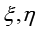
)对坐标系(x,y)的显式关系，用式（1.108）无法直接进行计算，只能采取逆运算方式。根据链式求导法则，可以得到
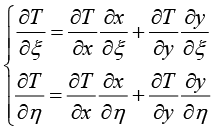（1.109）
将式（1.109）写成矩阵形式，即
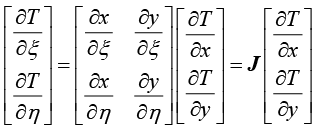（1.110）
其中，雅可比矩阵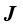
的计算公式为
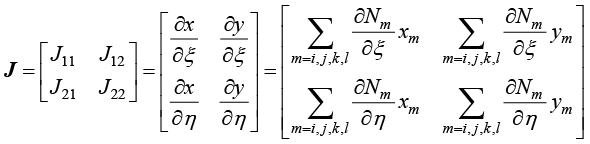（1.111）
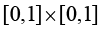正方形单元向任意四边形单元映射的雅可比矩阵为
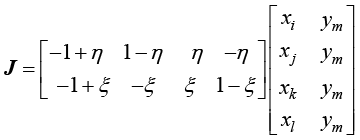（1.112）
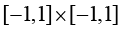正方形单元向任意四边形单元映射的雅可比矩阵为
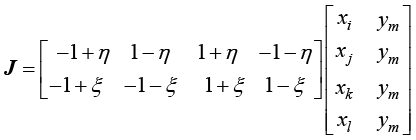（1.113）
由式（1.110）可得
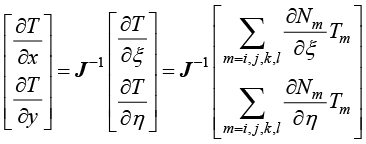（1.114）
为了计算雅可比矩阵的逆矩阵，先计算雅可比矩阵行列式，即
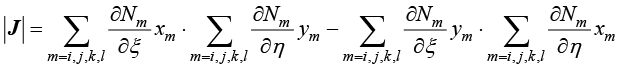（1.115）
根据矩阵求逆方法，雅可比矩阵的逆矩阵为
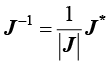（1.116）
其中，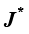
称为雅可比矩阵的伴随矩阵，按照以下方式计算：
（1.117）
同理，迦辽金权函数取为
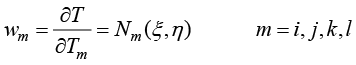（1.118）
迦辽金加权系数对全局坐标(x,y)的偏导数为
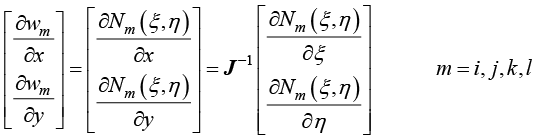（1.119）
为了书写方便，在后续章节中节点形函数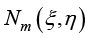
简记为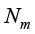
。
有限元法将物理空间中任意四边形单元温度刚度矩阵元素对全局坐标函数的计算方式转化为在参数空间中正方形单元对局部坐标的计算方式，即
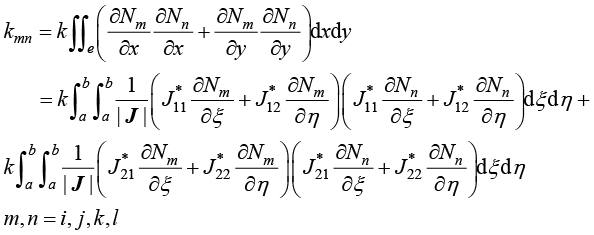（1.120）
参数空间中的积分上下限分别为正方形的坐标变化范围，对于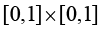正方形，a=0，b=1；对于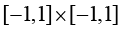正方形，则a=−1，b=1。
物理空间中任意四边形单元热容矩阵元素也可以在参数空间的正方形单元中进行计算，即
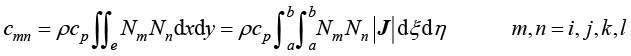（1.121）
物理空间中任意四边形单元中内热源产生的节点载荷也在参数空间中进行计算，即
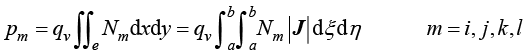（1.122）
二维参数空间中，任意函数的面积积分可以采用下面的数值积分方式进行计算：
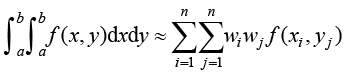（1.123）
4节点四边形单元同3节点三角形单元一样，每条边只有两个节点。因此，4节点四边形边界条件的计算方式与3节点三角形边界条件计算方式相同（具体见1.6.3节）。
许多传热现象与流体流动相关，如对流传热，这里简单介绍流体流动所遵循的物理定律，它们是建立流体运动基本方程组的依据。这些定律主要包括质量守恒定律、动量守恒定律、能量守恒定律、热力学第二定律，加上状态方程、本构方程。在实际计算时，还要考虑不同的流态，如层流与湍流。
在流场中，流体通过控制面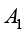
流入控制体，同时会通过另一部分控制面
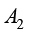流出控制体，在这期间控制体内部的流体质量也会发生变化。按照质量守恒定律，流入的质量与流出的质量之差，应该等于控制体内部流体质量的增量，由此可导出如下的流体流动连续性方程。
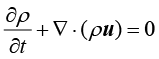（1.124）
其中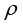，表示密度；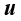
表示速度矢量。该式根据不同情况有不同形式，如对于不可压缩流体，该式可简化为
。
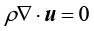动量守恒是流体运动时应遵循的另一个普遍定律，描述为：在一个给定的流体系统中，其动量的时间变化率等于作用于其上的外力总和，其数学表达式即为动量守恒方程，也称为运动方程，或N−S方程，其微分形式表达为
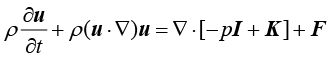（1.125）
其中，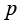
是压力；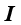
是单位矩阵；K为黏性应力张量；F是体积力矢量。
动量守恒方程在实际应用中有许多表达形式，需要根据实际计算情况来选择使用。
将热力学第一定律应用于流体运动中，得到如下的能量守恒方程（或流体的传热方程）。
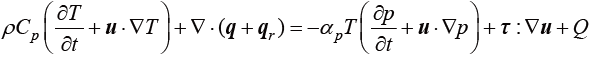（1.126）
其中，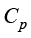
是恒定应力下的比热容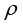；表示密度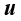；为平移运动速度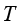；是绝对温度；
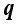是传导热通量；
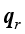为辐射热通量；
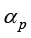是热膨胀系数，
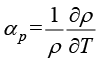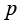；是压力；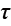
是黏性应力张量，包含黏性耗散以外的热源。
流动传热控制方程组的未知量主要有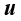、、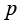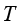，与方程数目相对，方程组封闭。但动量守恒方程中的惯性力项和能量守恒方程中的对流项是非线性的，并且动量微分方程和能量微分方程通常需要耦合求解，故直接求解是相当困难的。
湍流是自然界广泛存在的流动现象，湍流流动的核心特征是其在物理上近乎于无穷多的尺度和数学上强烈的非线性，这使得学者们无论是通过理论分析、实验研究还是计算机模拟来彻底认识湍流都非常困难，因此研究湍流机理，建立相应的模式，并进行适当的模拟仍是解决湍流问题的重要途径。COMSOL Multiphysics（以下简称COMSOL）提供的湍流模型包括代数yPlus模型、L-VEL模型、Spalart-Allmaras模型、标准k-ε模型、可实现的（realizable）k-ε模型、低雷诺数k-ε模型、k-ω模型、SST模型和v2-f模型等。
选取湍流模型时，需要考虑的因素包括流体是否可压、针对特定问题的习惯解法、精度的要求、计算机的计算能力、时间的限制。COMSOL还有壁面函数、自动壁面处理、湍流模型间自动切换等方式和方法帮助用户解决湍流求解问题。
Spalart-Allmaras模型增加了一个额外的无衰减运动学涡流黏度变量。它是一个低雷诺数模型，可求解实体壁之内的整个流场。这个模型最初针对空气动力学应用而开发，其优势在于相对稳健，分辨率要求不高，内存需求小，具有良好的收敛性，不使用壁面函数便可精确计算力（升力与曳力）、流量（传热与传质）。该模型不能精确计算包含剪切流、分离流或衰减湍流的流场。
L-VEL和代数yPlus湍流模型仅基于局部流速和与最近壁面的距离来计算湍流黏度，它们不求解附加变量。这两种模型的鲁棒性好，且计算强度低。虽然它们是精度较低的模型，但对内部流动却有很好的近似，尤其是在电子冷却应用中。
标准k-ε模型求解了两个变量：湍流动能k和湍流动能耗散率ε。本模型使用了壁面函数，但壁附近的解不够精确。标准k-ε模型具有稳定、很好的收敛速率和相对较低的内存要求，在工业领域应用广泛。标准k-ε模型可以在壁附近使用较粗的网格，对于复杂几何形状外部流动问题的求解效果很好，如标准k-ε模型可用于求解钝体周围的气流。但它不能精确地计算流动或射流中的逆压梯度和强曲率的流场。
标准k-ε模型的湍流动能k和耗散率ε的方程为
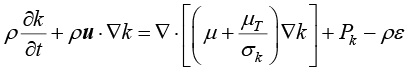（1.127）
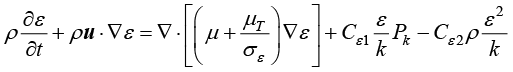（1.128）
其中，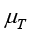
为湍流黏度，
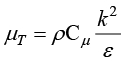；常数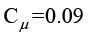
，
，
，
，
；
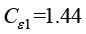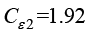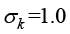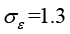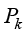为产生项，其表达式为
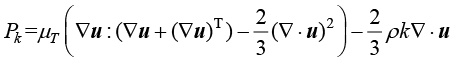（1.129）
可实现的k-ε模型与标准k-ε模型相比，有两个主要不同点：其一，可实现的k-ε模型为湍流黏性增加了一个公式；其二，为耗散率增加了新的传输方程，该方程来源于为层流速度波动而作的精确方程。除强旋流过程无法精确预测外，其他流动都可以使用此模型来模拟，包括有旋均匀剪切流、自由流（射流和混合层流动）、腔道流动和边界层流动。
k-ω模型通过两个输运方程求解k与ω。对于有界壁面和低雷诺数的可压缩性和剪切流动，该模型能取得较好的模拟效果，尤其适合处理圆柱绕流、放射状喷射、混合流动等问题，它包含转捩、自由剪切和压缩性选项。
SST模型结合了自由流中的k-ε模型和近壁的k-ω模型。它是一个低雷诺数模型，在工业应用中是一个“万能”模型。在对分辨率的要求方面，该模型与k-ω模型和低雷诺数k-ε模型相似，但消除了k-ω模型和k-ε模型表现出的一些弱点。
低雷诺数k-ε模型类似于标准k-ε模型，但没有使用壁面函数。它求解了每个位置的流动，是对标准k-ε模型的合理补充，拥有和后者一样的优势，但通常要求网格更加密集；它的低雷诺数属性不仅表现在壁面上，而且在各处都发挥作用，使湍流衰减。该模型有两种常用的方法：一种方法是首先使用标准k-ε模型计算出一个良好的初始条件，然后用它求解低雷诺数k-ε模型；另一种方法是使用自动壁面处理功能，首先利用粗化的边界层网格来获取壁面函数，然后对所需壁面处的边界层进行细化，进而获得低雷诺数k-ε模型。
低雷诺数k-ε模型可以计算升力和曳力，而且热通量的建模精度远远大于标准k-ε模型。在许多情况中，它表现出了卓越的预测分离和黏附的能力。
在接近壁面边界的地方，平行方向上的速度脉动通常会远远大于垂直于壁面的方向，速度脉动被认为是各向异性的。在远离壁面的地方，所有方向的脉动大小均相同，速度脉动变为各向同性。
除了使用两个分别描述湍流动能k和耗散率ε的方程，v2-f湍流模型还使用两个新方程来描述湍流边界层中湍流强度的各向异性：第一个方程描述了垂直于流线的湍流速度脉动的传递；第二个方程解释了非局部效应，例如由壁面引起的、垂直和平行方向之间的湍流动能的再分配阻尼。
大涡模拟（large eddy simulation，LES）用于解析较大的三维非定常湍流涡，而小涡流的影响则通过近似方法表示。这项技术与边界层网格划分一起使用时，可以精确描述瞬态流场以及边界上的精确通量和力。COMSOL中提供的LES模型包括“基于残差的变分多尺度”（RBVM）、“基于残差的黏性变分多尺度”（RBVMWV）和Smagorinsky模型。
在流体动力学计算中，初始条件和边界条件的正确设置是关键的一步。COMSOL软件提供了现成的各种类型的边界条件。
初始条件是计算初始给定的参数，即t=t0时给出各未知量的函数分布。初始条件需要根据实际情况设置。当流体运动定常时，无初始条件问题。
边界条件是流体力学方程组在求解域的边界上流体物理量应满足的条件。例如，流体被固壁所限，流体就不应有穿过固壁的速度分量；在水面边界上，大气压强认为是常数（一般在距离不大的范围内可如此）；在流体与外界无热传导的边界上，流体与边界之间无温差等。虽然各种具体问题不同，但边界条件一般要保持恰当：①保持在物理上是正确的；②要在数学上不多不少，刚好能用来确定微分方程中的积分常数，而不是矛盾的或随意性的。
流动方程的有限元求解方法与前面传热有限元分析类似，所不同的是速度与压力的插值函数不一样。这里以牛顿流体流动的有限元分析为例，介绍流动方程的有限元求解思路。
对于图1-9所示的带有小入口与出口的矩形区域（尺度为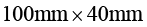
）内牛顿流体的流动问题，进行有限元求解，已知流体黏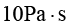度为
，密度为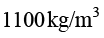
，入口给定压力
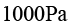，出口敞开。
图1-9 带有小入口和出口的矩形流动区域
考虑惯性项影响的N-S方程组（包含连续性方程与运动方程）表示如下。
连续性方程的表达式为
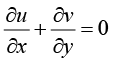（1.130）
运动方程的表达式为
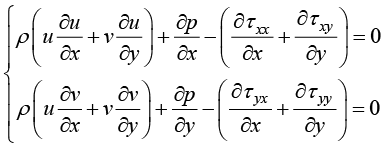（1.131）
其中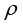，为流体密度。切应力的计算公式为
（1.132）
将式（1.132）代入式（1.131），得到
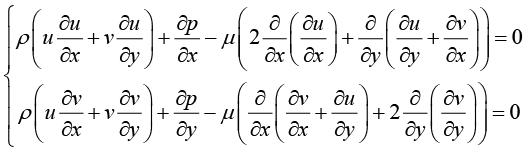（1.133）
边界条件包括速度和压力两种。入口给定压力，出口敞开，即给定法向压力边界条件：
；
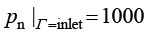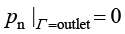（1.134a）
在壁面无滑移假设的情况下，速度边界条件为
；
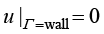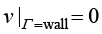（1.134b）
（1）计算区域的离散。采用四边形网格对计算区域进行离散。速度单元采用四边形二次单元（9节点），压力单元采用四边形线性单元（4节点）。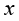
方向单元数量为12，
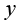方向单元数量为12。离散后单元总数为144，速度单元节点总数为625，压力单元节点总数为169。底部和右侧下部壁面组成了边界1，右侧上部开口处为边界2，顶部和左侧上部组成了边界3，左侧下部开口处为边界4，如图1-10所示。
图1-10 网格及边界图
（2）插值函数及其相关计算。确定离散单元类型后，单元内任意一点的速度和压力可分别表示为
，
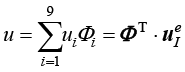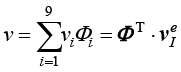（1.135）
（1.136）
其中，插值函数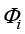
和
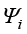的表达式为
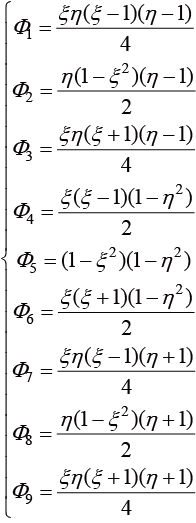（1.137）
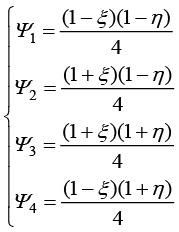（1.138）
（3）加权余量方程。这里的加权余量方程是指连续性方程的加权余量方程和运动方程的加权余量方程。其中，连续性方程的加权余量方程为
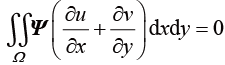（1.139）
运动方程的加权余量方程采用迦辽金有限元方法，权函数等于插值函数。将式（1.133）与权函数相乘，并在计算区域内积分，得到
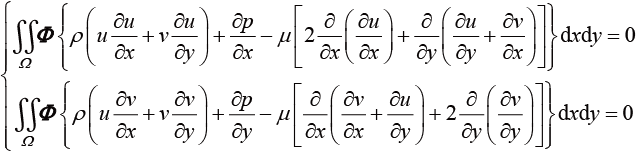（1.140）
将惯性项中的密度提出后，得到惯性项展开方程，即
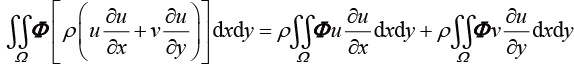（1.141）
（4）单元方程的建立。这里的单元方程是指连续性方程的单元方程和运动方程的单元方程。将连续性方程的加权余量方程的积分区域由总体区域转变为单元区域，并将式（1.135）代入，得到连续性方程的单元方程：
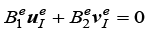（1.142a）
其中，
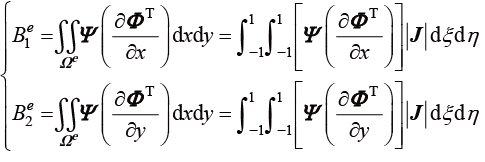（1.142b）
将式（1.140）的积分区域由总体区域转变为单元区域，并将式（1.135）和式（1.136）代入运动方程各项，得到运动方程的单元方程：
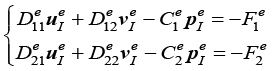（1.143a）
其中，各项表达式如下：
（1.143b）
惯性项计算中，需要已知流体密度。惯性项离散方法可以采用速度项提出法，即
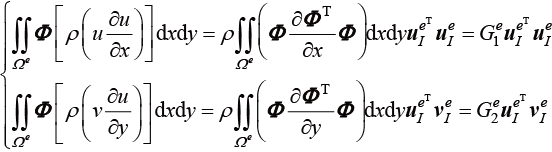
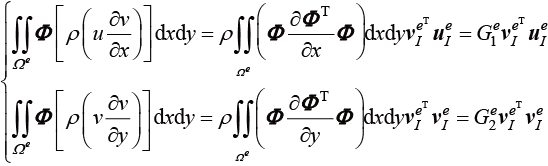（1.144）
其中，
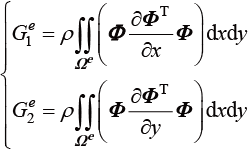（1.145）
对应单元的方程表示为
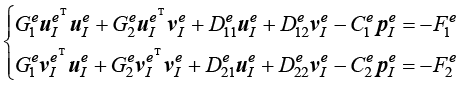（1.146）
（5）总体方程的组合。根据单元方程子块组合总体方程子块的相关内容，对单元方程进行组合，可得到总体方程。连续性方程的总体方程表示为
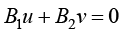（1.147）
运动方程的总体方程表示为
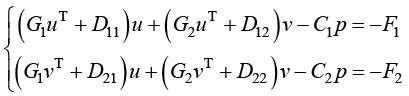（1.148）
总体方程的矩阵形式为
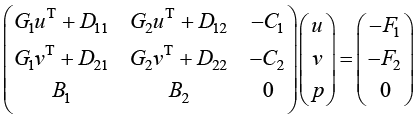（1.149）
上述方程组是非线性方程组，可以采用牛顿-拉弗森（Newton-Raphson）迭代法或线性化交替迭代法求解，详细请见参考文献[2]。
工程实践中有许多耦合传热问题，如热固耦合、相变传热、蒸发与冷凝、多孔介质传热、电磁传热（含电阻热、感应加热、微波加热）等。
固态传热问题通常涉及热固耦合，既要研究传热问题以确定温度场，又要研究固体受热膨胀引发的热应力问题。热固耦合有直接耦合与顺序耦合两种方式，直接耦合是将温度场与应力场（变形场）完全耦合，顺序耦合是先计算温度场，然后将其作为载荷耦合入应力场的研究中。在大多数情况下，传热问题所确定的温度将直接影响固体的热应力，而应力场对温度场影响不大，故多采用顺序耦合（单向耦合）作为热固耦合问题的分析方法。对于温度引起的热应力，主要体现在固体物理方程的变化（如热膨胀引起的应变量），下面以线弹性材料为例，说明固体物理方程（或本构方程）的变化。
对于线弹性材料的某物体，其内部存在温差分布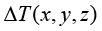
，在温差的作用下，该物体会产生热膨胀，其热膨胀量为
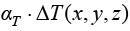，αT为热膨胀系数，则该物体的物理方程由于增加了热膨胀量（正向的温度应变）而变为式（1.150）。
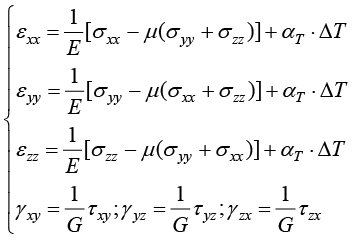（1.150）
其中，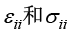
分别为正应变和正应力，
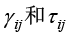分别为切应变和切应力，E、μ和G分别为弹性模量、泊松比和剪切模量。
自然界中的物质按聚集态分为固、液、气三相，相变是物质在外部参数（如温度、压力、磁场等）连续变化下，从一种相突然变为另外一种相，如冰变成水或水变成蒸汽等。物体相变会释放或吸收热量。
相变过程的傅里叶方程可表示为
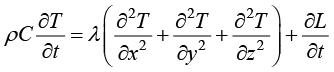（1.151）
其中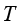，为温度；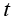
为时间；x、y、z为空间坐标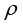；为密度；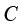
为比热容；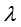
为导热系数；
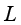为潜热。
式（1.151）的左侧是相对于该温度变化的热量；等号右侧第一项为热流过程中由流入微元体和流出微元体的差造成的热量增量（堆积）；第二项为单位体积单位时间内凝固时释放的潜热或熔化时吸收的潜热，可视其为特殊的热源。
根据热力学知识，焓和比热容密切相关，而潜热是纯相变导致的热焓变化量，故在利用有限元等方法求解相变过程热平衡方程时，一般按等效热容方式处理。在COMSOL中也是按这种方式处理，通过捕捉相变界面各相分数，按等效热容考虑相变潜热。
图1-11为两相相变过程，即相变温度、相变温度间隔示意。其中，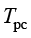
为相变转变温度；
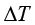为相变温度间隔，实际相变温度区间为
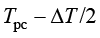到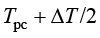
；
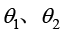分别为两相分数，若将
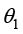定义为
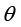，则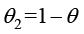
。
图1-11 相变温度、相变温度间隔示意
等效密度与等效热焓的表达式为
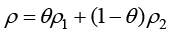（1.152）
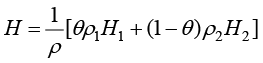（1.153）
其中，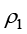
、
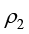分别为两相密度；
、
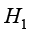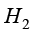分别为两相基于参考温度的焓。
比热容的表达式为
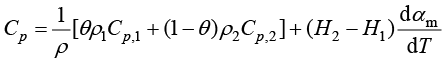（1.154）
其中，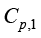
、
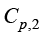分别为两相比热容；
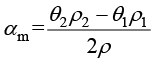，表示质量分数，反映相变进程。
将式（1.154）等号右侧拆分成两项，并将其分别定义为
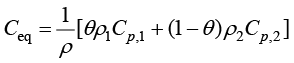（1.155）
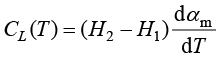（1.156）
式（1.155）表示对两相（如固液）比热容进行等效加和，式（1.156）表示相变潜热对等效比热容的贡献，潜热为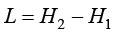
，故有
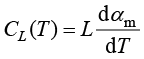（1.157）
在相变温度区间内公式（1.157）闭环（该式在相变温度区间内的积分为L），在等效算法中能量始终守恒。
实际分析中，在相变界面处，物质的等效热容、等效导热系数、等效密度的表达式为
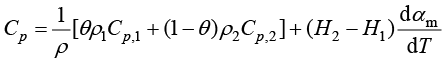（1.158）
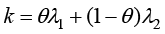（1.159）
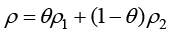（1.160）
其中，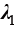
、
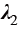分别为两相的导热系数。对于未发生相变区域，仍然采用单相材料参数进行计算。
模拟液体（例如水）的蒸发冷却过程，需要考虑3个效应：周围空气的湍流、所有域中的传热、空气中液体的输送。
在COMSOL中使用“湍流，低雷诺数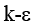
”接口模拟气流，同时要在输运方程中正确考虑湍流效应。使用低雷诺数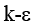湍流模型，湍流变量在整个域中求解，因此输运方程的输入值需要准确。设速度场和压力场与空气温度和湿度无关，在此设定下预先计算湍流场，然后将其用作传热和物质输运方程的输入。由于液面上蒸发引起的质量贡献很小，因此在此边界上使用壁（无滑移）条件来计算气流。
容器和液体中的传热仅通过传导进行，湿空气中的传导方式主要是对流传热，且需要湍流场，材料属性由湿空气理论决定。
蒸发过程中，除周围的对流和传导冷却外，还会从液面释放潜热，引起液体冷却，这个额外的热通量取决于蒸发的液体量。潜热源的表达式为
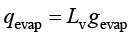（1.161）
其中，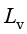
为蒸发潜热，单位为J/kg；
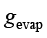为蒸发通量。
为了获得蒸发到空气中的确切液体量（水量），使用“空气中的水分输送”接口。初始相对湿度为20%。水表面发生蒸发，蒸发通量的表达式为
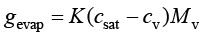（1.162）
其中，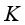
为蒸发率；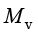
为水蒸气摩尔质量；
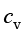为水蒸气浓度；
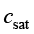为饱和浓度，其计算公式为
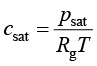（1.163）
输运方程再次使用湍流场作为输入。扩散系数中还必须考虑湍流的影响，即将下式湍流扩散系统添加到扩散张量中。
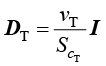（1.164）
其中，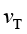
为湍流运动黏度；
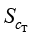为湍流施密特数；I为单位矩阵。
多孔材料存在大量孔隙可以容纳流体，称为多孔介质，在机械、航空航天、环境、冶金、电子、建筑等多个领域有广泛应用。多孔介质在传热中发挥着重要作用，通常要分析多孔介质的热性能。
以注入比多孔介质温度高得多的流体为例，多孔介质的温度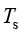
和流体的温度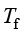最初不相同，随着时间变化逐渐达到平衡。在许多应用中，
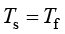假设成立，称其为（局部）热平衡，而在某些应用中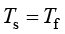的假设不成立，称为（局部）热非平衡，“局部”是指温度逐点比较。
在局部热平衡假设下，描述整个多孔介质内平均温度只需一个方程。根据能量守恒以及应用混合规则，热传递方程式可以表达为
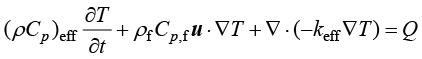（1.165）
流体和多孔介质的热特性有效体积热容和有效导热率计算公式为
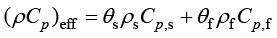（1.166）
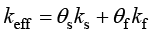（1.167）
其中，f、s分别代表流体和固体；k、ρ分别为导热系数和密度；Cp为恒压下的热容；θ为体积分数。假定多孔介质为完全饱和的，孔隙率对应于流体的体积分数。
在COMSOL中，热平衡下的多孔介质传热场可以通过传热模块的多孔介质传热选项添加。
局部热平衡有时无法达到，尤其是快速的非等温流动，在较短时间尺度或强烈依赖于其他影响（如相变）的情况下，固体和流体温度之间的差异可能很大。此时等式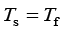
并不完全有效，必须分别考虑各相的能量平衡，并且以显式考虑两相之间的热交换，这是通过两个温度模型完成的。局部热非平衡方法求解了两个温度场，并通过热源将它们耦合。
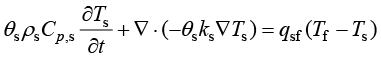（1.168）
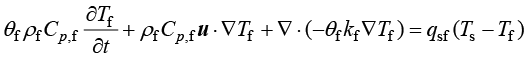（1.169）
固体与流体之间的热交换由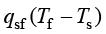
决定，其中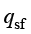
是间隙热传递系数，其取决于相的热性质及多孔介质的结构（接触的表面积）。
在COMSOL中，热非平衡下的多孔介质传热场可以通过多物理场中的局部热非平衡选项添加。
另外，涉及多孔介质的应用还有地下水传热、裂隙流和多孔弹性等问题，可阅读文献[21]。
电气设备的性能与温度相关，在电磁数值分析中往往会遇到电磁传热问题，包含热量的输入，避免因电磁损耗产热等。这里主要介绍COMSOL系统内置的典型电磁热源的多场耦合接口的基础理论，包含焦耳热、感应加热和微波加热等。
电流在流经电阻时，载流导体中能够产生热量，电能转化为热能的过程称为焦耳热（或电阻加热、欧姆加热）。在使用COMSOL进行焦耳热分析时，焦耳热多物理场接口耦合了固体传热和电流接口，包含了传导电流和介电损耗所产生的热量。
焦耳热接口模拟电阻装置，产生的主要是电阻热，将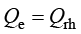
添加为热源时：
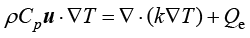（1.170）
在频域中：
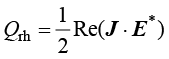（1.171）
在时域中：
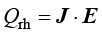（1.172）
在频域中采用电导率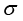和复数相对介电常数
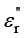表示材料的损耗。
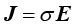（1.173）
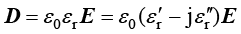（1.174）
以电加热板为例，电加热板由沉积在玻璃板上的电阻层组成，玻璃板下面是待加热的反应流体，当电路施加电压时，电阻内部就会产生焦耳热，然后将热量传递到流体中，装置产生的热量由电阻层决定。
在电加热板模拟中，利用固体传热和多层壳中的电流耦合对电加热板进行作用。在COMSOL系统中，使用焦耳热物理场时，需要添加“多层壳中的电流”和“固体传热”接口。薄层内产生的单位面积热耗率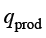
（单位为W/m2）计算公式为
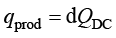（1.175）
其中，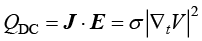
为功率密度，产生的热量在玻璃板表面表现为向内热通量。
感应加热是利用电磁感应的方法使被加热的材料内部产生涡流，依靠这些涡流的能量实现加热，通常用于金属加工、热处理、焊接与熔化等场合。感应加热系统主要由感应线圈、交流电源和工件组成，线圈与电源相连，电源为线圈提供交变电流，流过线圈的交变电流产生一个交变磁场，该磁场使工件产生涡流来加热。这是一种非接触的加热方式，加热产生的热量集中在工件内部，再作用于工件，加热效率很高。
在COMSOL中使用感应加热接口对交流线圈中的铁磁体芯建模时，需耦合固体传热与磁场接口，主要考虑了由于感应电流和磁损耗产生的热量，将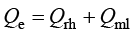
添加为热源项。
在频域中：
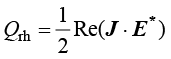（1.176）
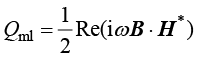（1.177）
在时域中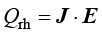，，而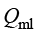
与磁滞模型有关；在频域中，用电导率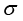表示材料的电阻损耗，并对B和H的关系进行线性化处理，用复磁导率
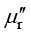表示材料的磁损耗：
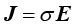（1.178）
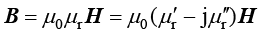（1.179）
微波加热是涉及电磁波和传热的多物理现象，任何暴露在电磁辐射中的材料都会被加热。物质在微波场中所产生的热量大小与物质种类及其介电特性有很大关系，即微波对物质有选择性加热的特性。
在COMSOL中，微波加热多物理场接口耦合了“生物传热”与“电磁波，频域”接口，它考虑了高频状态下由电阻、电介质和磁损耗产生的热量。例如，使用微波加热接口对治疗肿瘤进行模拟时，也是将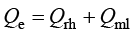添加为热源项。在频域中，
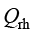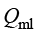、的表达式分别与式（1.176）和式（1.177）相同。
应用有限元法分析工程实际问题的一般过程如图1-12所示，通常分为3个阶段，即前处理（preprocessing）、分析（analysis）和后处理（post processing）。
图1-12 应用有限元法分析工程问题的一般过程
有限元分析的第一阶段是把工程实际问题转化为可供计算机分析的有限元模型。有限元模型的合理性、正确性将直接影响计算分析结果与工程实际之间的差距。这一过程称为有限元分析的前处理过程，通常称为有限元建模过程。显然，有限元建模是应用有限元法解决工程问题的关键。有限元建模主要包括三方面的内容：一是要构造计算对象的几何模型（确定所求问题的类型，建立分析对象的力学模型）；二是要划分有限元网格（包括单元类型的选择，网格的布局）；三是要生成有限元分析的输入数据（主要包括材料与边界条件数据）。建立一个符合工程要求的力学模型，不是一件轻而易举的事情，不仅要有宽广的力学知识和工程背景知识，还取决于有限元计算经验的积累和对分析对象了解的深入程度。
有限元分析过程主要是建立各类问题的有限元方程，并求解这些方程。通过单元分析、整体分析、载荷移置、引入约束即可得到有限元方程，这是有限元分析的核心内容。而对所建立的有限元方程，选择合适的方法求解，也是有限元理论中要重点讨论的内容。
后处理主要包括计算结果的加工处理、计算结果的可视化（图形显示）、计算结果的打印。它把有限元分析得到的数据转换为工程师直接需要的信息，如温度分布状况、流动情况、结构变形状态等，从而帮助工程师快速地评价和校核设计方案。
对于需要系统学习有限元理论的初学者，必须全面掌握上述内容。而对仅使用有限元软件解决工程实际问题的技术人员，其主要工作体现在前处理与后处理两个阶段，但对分析过程也应大致了解。因为有限元软件只是提供一个数值分析的黑箱，如果没有有限元理论的基本知识，面对软件中的许多选择或参数确定就会感到束手无策、无所适从，甚至会使数值分析结果完全偏离工程实际，得到错误结论。
有限元法的分析过程依赖于假定的单元插值函数，为了得到满意的解答，必须使假定的单元插值函数尽可能逼近计算域物理量的真实分布。如果假定的单元插值函数（对于弹性力学问题是位移函数）与物理量的真实分布完全一致，有限元解便是精确解。一般找不到（或很难找到）真实物理量分布情况，所以只能得到近似解答。
单元插值函数一般采用包含若干待定参数的多项式作为近似函数，称为插值多项式。有限项多项式选取的原则应考虑以下几点。
（1）待定参数是由节点场变量确定的，因此待定参数的个数应与单元的自由度数相同。
（2）插值函数在单元内要保持连续，应提供单元间的连续性，包含离散单元每一个节点所有自由度都是连续的。
（3）多项式的选取应由低阶到高阶，尽量选取完整性阶数高的多项式以提高单元精度（称为单元的完备性）。若由于项数限制不能选取完整多项式，选取的多项式应尽可能具有坐标的对称性（称为几何不变性）。对于弹性力学问题，插值函数（多项式）应考虑刚体位移和单元内的常应变状态；插值函数在相邻单元的公共边界上必须协调。
有限元法是一种数值方法，因此应考虑该方法的收敛性问题。有限元法的收敛性是指当网格逐渐加密时，有限元解答的序列收敛到精确解；当单元尺寸固定时，每个单元的自由度数越多，有限元的解答就越趋近于精确解。
有限元法在解决由扩散驱动的传递问题时比较稳定，但处理以对流为主的传递问题时，往往会发生数值不稳定性，即解的振荡现象。以典型的对流扩散传递方程为例，即
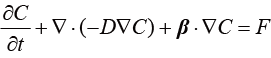（1.180）
其中，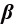
为对流速度；
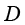为扩散系数；
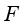为源项。研究发现，对于具有一阶形状函数的均匀网格，当Peclet数
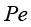超过1时，会发生数值不稳定：
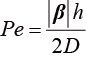（1.181）
其中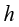，为单元尺寸。
Peclet数与对流和扩散效应有关，大的对流或小的扩散都会导致Peclet数大于1，同时单元大小也起着重要作用。单元（网格）分辨率越高，Peclet数越小，故对于每个非零扩散项，存在一个单元分辨率，使整个计算域中的Peclet数小于1。但这样的单元计算很昂贵，甚至不可行。稳定方法允许在更粗的网格上进行模拟，从而大大减轻了计算负荷。在COMSOL中，所有传递接口，如传热、流体流动或物质传递，都会自动使用稳定性工具。
作为人工智能的一个分支，机器学习是一个涉及概率论、统计学、凸分析和其他学科知识的跨领域学科。机器学习使用一些特定算法从历史数据中学习，构建预测模型，无须显式的物理模型对未知结果做出预测，侧重于从数据中获取信息。它可以解决一些高度非线性的问题，而无须很多人为的干预。通常机器学习方法分为监督学习和无监督学习，分类和回归属于前者，聚类属于后者，两种类别之间最大的差异是：监督学习方法的训练数据由输入和相应的预期输出组成，而无监督学习方法中的训练数据没有预期输出。回归场合中常用的机器学习方法包括线性回归、支持向量回归、最小二乘回归等。决策树、支持向量机和朴素贝叶斯是用于分类目的的主流机器学习算法；此外，神经网络和极限学习机可用于分类和回归。机器学习在很多领域得到应用，如产品加工监测、计算机视觉、智能医疗服务、智能交通、数据挖掘、智能制造、数值分析和专家系统等方面。
一些学者利用机器学习方法分析传热问题，如刘耀东等以兰州黄河桥为工程背景，使用具有复杂映射功能的人工神经网络研究混凝土桥梁结构温度场分布，根据温度场的影响因素数据采用三层前向BP网络建立温度场的求解算法，从而得到温度场的形成过程和分布规律。Yue等采用深度学习的方法建立结构温度与温度变形之间的映射关系模型，利用长短期记忆网络（long short-term memory，LSTM）和卷积神经网络的优势检测桥梁结构异常变形。王得道等采用卷积神经网络分析外界环境因素对结构温度的影响，之后采用长短期记忆网络对结构温度进行预测。Zhang等建立了一个同时预测超临界H2O和CO的壁面温度和努塞尔数Nu的通用AN模型，对Nu进行预测。Amardee等基于超临界水在垂直上升管道中换热的CFD模拟数据，利用AN对Nu进行预测，平均绝对百分比误差（mean absolute percentage error，MAPE）达到1.46%。Ma等在低热流密度工况下，建立了超临界水传热系数预测的反向传播神经网络（back propagation neural network，BPNN）模型，R2为0.971。Sun等使用遗传算法优化的反向传播神经网络（genetic algorithm optimization of back propagation，GA-BP）的初始参数，建立了GA-BP模型，对管内超临界CO流动传热的Tw进行预测，均方根误差（root mean square error，RMSE）达到1.03 ℃，R2达到0.99。Pesteei等人采用数据处理组法（group method of data handling，GMDH）模型预测了雷诺数Re<2500条件下垂直管内超临界CO的局部换热特性，RMSE=25.643 kW/（m2·K），R2=0.984。李浩哲等利用可解释机器学习进行了超临界流体传热特性预测与分析。张昂利用机器学习研究泉州湾高铁斜拉桥的桥塔温度与大气温度、太阳辐射强度、风速等环境因素的关系。刘成结合计算流体力学数据集，建立机器学习预测模型，并对高热流密度元器件散热器的热阻和压降进行了优化。王爱军利用支持向量机（机器学习的一种）对不同结构的轴承体在不同工况下所需的冷却水流量进行了预测，为轴承体结构设计和冷却策略提供了参考。吴哲建立了神经网络模型，实现了热−流耦合模型的实时求解，在测试集上的评价准确率达97.6%，并减少了训练数据量。吴浩等采用机器学习分析了高温气冷堆球床辐射传热问题。刘天赐将深度学习技术应用在对流传热分析中，解决了特征提取问题，提升了机器学习识别准确率与模型泛化能力。Qurrat Ul Ain等采用神经网络辅助研究了星形封闭内的混合纳米流动的强化传热问题。Seyedalborz Manavi等采用带参数化物理信息的机器学习方法求解干燥过程的传热传质问题。Darioush Jalili等利用融入物理信息的神经网络（physics-informed neural network，PINN）分析了两相液膜沸腾传热问题。洪亮等分别基于k近邻、决策树和AdaBoost机器学习算法预测燃料棒包壳外表面和燃料芯块中心温度。刘振海等采用机器学习方法构建了燃料棒温度分布的代理模型，快速预测燃料棒不同时刻的温度分布。从这些研究看到，机器学习方法能够为复杂的换热行为和传热特性提供更为准确的预测。
机器学习与传热有限元分析确实存在重叠，主要体现在以下几个方面。
（1）数据驱动的特性：传热有限元在进行模型设置时需要大量的实验数据和材料特性，而这些数据可以通过机器学习进行处理和分析，并优化模型参数。
（2）模型逼近：在一些高维和复杂的物理问题中，传热有限元模型可能计算代价高昂，而机器学习算法能够在某些情况下提供更快的近似解。通过训练数据学习，机器学习模型可以快速预测出与物理模型相似的结果。
（3）不确定性分析：传热有限元分析在处理材料属性和加载条件方面存在一些不确定性，机器学习可以通过概率模型（如贝叶斯方法）有效地处理这些不确定性，提高分析的可靠性。
尽管机器学习和传热有限元分析在某些方面存在重叠，但各自具有的优势使得它们能够在实际应用中互为补充。
（1）增强物理模型：机器学习可以帮助强化和修正传热有限元模型，基于已有的传热有限元结果，训练机器学习模型，能使其更好地捕捉复杂的物理现象。
（2）优化设计过程：将机器学习与传热有限元分析结合，能够加速设计优化过程。通过使用机器学习方法快速评估设计方案，结合传热有限元方法进行精确分析，能够有效缩短设计周期，尤其是传热参数优化与传热结构拓扑优化方面，可以利用机器学习协助寻求最优解。
（3）实时反馈与学习：在实际工程应用中，机器学习可以利用传热有限元分析的实时结果进行在线学习，及时调整模型和参数，提高系统的响应能力和适应性。
总之，在有限元的预处理、计算和后处理阶段，机器学习展现出了良好的适用性。在预处理阶段，机器学习算法如决策树和支持向量机（SVM）可以帮助进行自动化几何建模和网格划分。在计算阶段，人工神经网络（ANN）等深度学习工具可以通过处理复杂的非线性关系，大幅提高系统求解的速度与精度。在后处理阶段，机器学习方法能够帮助分析和解读结果，优化设计方案。
随着计算机科学和数据科学的不断发展，机器学习与传热有限元分析的结合将会变得越来越紧密。未来的发展方向可能包括以下几个。
（1）深度学习与模型简化：使用深度学习技术简化和加速复杂传热有限元模型的求解过程，实现实时模拟。
（2）数据融合与智能优化：将来自不同源的数据（如传感器数据、历史实验数据）与机器学习结合，实现更深入的智能优化设计。
（3）物理信息学习：物理信息机器学习（physics-informed machine learning，PIML）技术将物理规律嵌入机器学习过程，可以提高预测结果的可信度，目前PIML已经在传热分析中进行应用。
机器学习方法应用在传热分析方面有两大类思路，具体如下。
（1）直接植入实际问题的物理信息机器学习程序来求解传热分析问题。例如，利用PINN进行传热分析，先定义传热问题及物理模型；接着构建PINN模型结构，确定输入与输出物理量，设置多个隐藏层，每层使用激活函数（如tanh、sigmoid、ReLU等），某个PINN模型示例如图1-13所示；再定义损失函数，包含数据误差项和物理信息误差项，将偏微分方程、初始条件、边界条件嵌入神经网络的损失函数中；接着利用数据进行神经网络训练，使用梯度下降或其他优化算法对网络权重进行调整，并通过最小化损失函数，使神经网络的输出满足给定的偏微分方程和条件；最后对训练好的模型进行验证与测试，确保模型在训练集以外的数据上也能做出准确、符合传热规律的预测。
图1-13 PINN模型示例
（2）将机器学习方法与有限元方法融合来进行传热分析，以大幅提升传热分析效率与降低分析成本。机器学习方法与有限元方法融合的方式较多，其中一种是：利用有限元分析生成大量的训练数据，再导入机器学习算法（如深度神经网络、支持向量机等）中进行训练，生成代理模型，代理模型（输入与输出的近似函数）可以快速实现输入与输出的映射。
COMSOL系统中的代理模型训练，是将机器学习方法与有限元方法有效融合，用来便捷地建立输入数据与输出数据之间复杂的非线性映射关系，即用代理模型替换复杂的有限元模型，降低计算成本和缩短分析时间，具体在6.4.1节中详细叙述。
